新人教A版选修4-5 3.1二维形式柯西不等式练习卷
实数ai(i=1,2,3,4,5,6)满足(a2﹣a1)2+(a3﹣a2)2+(a4﹣a3)2+(a5﹣a4)2+(a6﹣a5)2=1则(a5+a6)﹣(a1+a4)的最大值为( )
| A.3 | B.2 |
C. |
D.1 |
二维形式的柯西不等式可用( )表示.
| A.a2+b2≥2ab(a,b∈R) |
| B.(a2+b2)(c2+d2)≥(ab+cd)2(a,b,c,d∈R) |
| C.(a2+b2)(c2+d2)≥(ac+bd)2(a,b,c,d∈R) |
| D.(a2+b2)(c2+d2)≤(ac+bd)2(a,b,c,d∈R) |
 +
+ +
+ 的最大值是( )
的最大值是( )






 +b
+b =1,则以下成立的是( )
=1,则以下成立的是( ) )x+ky≥
)x+ky≥ 恒成立,则实数k的最小值是( )
恒成立,则实数k的最小值是( ) 的最大值为( )
的最大值为( )
 +
+ 的最小值为( )
的最小值为( )





 ,
, ),且满足
),且满足 =
= ,
, +
+ =
= ,则
,则 的值为( )
的值为( )

 +3
+3 <k
<k 恒成立,利用柯西不等式可求得实数k的取值范围是 .
恒成立,利用柯西不等式可求得实数k的取值范围是 . 的最大值是 .
的最大值是 . +
+ +
+ c的最大值是 ,此时a+b+c= .
c的最大值是 ,此时a+b+c= . +
+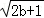 +
+ 的最大值为 .
的最大值为 . =(a,b),
=(a,b), =(m,n),其中a,b,m,n∈R,由不等式|
=(m,n),其中a,b,m,n∈R,由不等式|
 |
| •|
•| |恒成立,可以证明(柯西)不等式(am+bn)2≤(a2+b2)(m2+n2)(当且仅当
|恒成立,可以证明(柯西)不等式(am+bn)2≤(a2+b2)(m2+n2)(当且仅当 ,即an=bm时等号成立),己知x,y∈R+,若
,即an=bm时等号成立),己知x,y∈R+,若 恒成立,利用柯西不等式可求得实数k的取值范围是 .
恒成立,利用柯西不等式可求得实数k的取值范围是 . 粤公网安备 44130202000953号
粤公网安备 44130202000953号