分12分)已知椭圆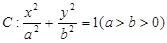 过点
过点 ,且离心率
,且离心率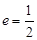 。
。
(1)求椭圆方程;
(2)若直线 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、 ,且线段
,且线段 的垂直平分线过定点
的垂直平分线过定点 ,求
,求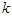 的取值范围。
的取值范围。
满分12分)已知函数f(x)=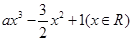 ,其中a>0.
,其中a>0.
(Ⅰ)若a=1,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)若在区间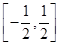 上,f(x)>0恒成立,求a的取值范围.
上,f(x)>0恒成立,求a的取值范围.
满分12分)已知曲线C :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(Ⅰ)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(Ⅱ)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到
到
直线 (t为参数)距离的最小值。
(t为参数)距离的最小值。
满分12分)已知抛物线的顶点在原点,它的准线过双曲线 ,(
,( )的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点
)的一个焦点,且这条准线与双曲线的两个焦点连线互相垂直,又抛 物线与双曲线交于点 ,求抛物线和双曲线的方程.
,求抛物线和双曲线的方程.
某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动,已知3月份达到最高
价格8元,7月份价格最低为4元. 该商品在商店内的销售价格在8元基础上按月份
随正弦曲线波动,5月份销售价格最高为10元,9月份销售价最低为6元.
(1)试分别建立出厂价格、销售价格的模型,并分别求出函数解析式;
(2)假设商店每月购进这种商品m件,且当月销完,试写出该商品的月利润函数;
(3) 求该商店月利润的最大值。
利用“五点法”画出函数 在长度为一个周期的闭区间的简图,
在长度为一个周期的闭区间的简图,
并说明该函数图象可由y=sinx(x R)的图象经过怎样
R)的图象经过怎样 平移和伸缩变换得到的。
平移和伸缩变换得到的。
( 本题16分)如图,某大风车
本题16分)如图,某大风车 的半径为2米,每12秒沿逆时
的半径为2米,每12秒沿逆时 针方向旋转一周,它的最底点
针方向旋转一周,它的最底点 离地面1米,风车圆周上一点A从最底点
离地面1米,风车圆周上一点A从最底点 开始,运动t秒后与地面距离为h米,
开始,运动t秒后与地面距离为h米,
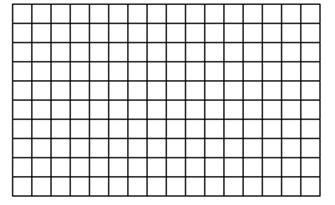
(1)求函数h =f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
=f(t)的关系式, 并在给出的方格纸上用五点作图法作出h=f(t)在一个周期内的图象(要列表,描点);
(2) A从最底点 开始, 沿逆时针方向旋转第一周
开始, 沿逆时针方向旋转第一周 内,有多长时间离地面的高度超过4米?
内,有多长时间离地面的高度超过4米?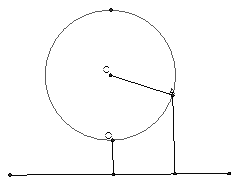
(本题16分)函数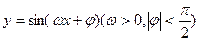 在同一个周期内,当
在同一个周期内,当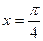 时
时 取最大值1,当
取最大值1,当 时,
时, 取最小值
取最小值 。
。
(1)求函数的解析式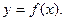
(2)函数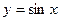 的图象经过怎样的变换可得到
的图象经过怎样的变换可得到 的图象?
的图象?
(3)若函数 满足方程
满足方程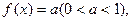 求在
求在 内的所
内的所 有
有 实数根之和.
实数根之和.
函数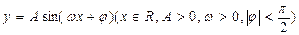 的
的 图象上相邻的最高点与最低点的坐标分别为M(
图象上相邻的最高点与最低点的坐标分别为M(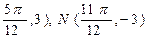 ,求此函数的解析式。
,求此函数的解析式。