设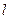 ,
,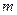 是两条不同的直线,
是两条不同的直线,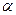 是一个平面,则下列命题正确的是( )
是一个平面,则下列命题正确的是( )
A.若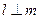 , ,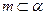 ,则 ,则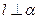 |
B.若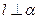 , ,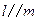 ,则 ,则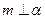 |
C.若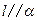 , ,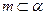 ,则 ,则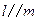 |
D.若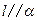 , ,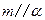 ,则 ,则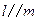 |
与正方体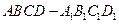 的三条棱
的三条棱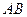 、
、 、
、 所在直线的距离相等的
所在直线的距离相等的
点 ( )
| A.有且只有1个 | B.有且只有2个 |
| C.有且只有3个 | D.有无数个 |
已知正四棱锥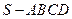 中,
中,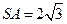 ,那么当该棱锥的体积最大时,它的高
,那么当该棱锥的体积最大时,它的高
为 ( )
| A.1 | B.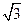 |
C.2 | D.3 |
已知三棱锥 中,底面
中,底面 为边长等于2的等边三角形,
为边长等于2的等边三角形,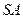 垂直于底
垂直于底
面 ,
,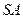 =3,那么直线
=3,那么直线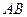 与平面
与平面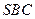 所成角的正弦值为( )
所成角的正弦值为( )
A. |
B.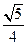 |
C. |
D.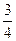 |
有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处
相连能够焊接成一个三棱锥形的铁架,则a的取值范围是 ( )
A.(0,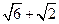 ) ) |
B.(1,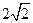 ) ) |
C.(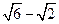 , ,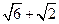 ) ) |
D.(0,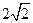 ) ) |
已知 是球
是球 表面上的点,
表面上的点,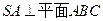 ,
, ,
,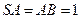 ,
, ,则球
,则球 的表面积等于 ( )
的表面积等于 ( )
A.4 |
B.3 |
C.2 |
D. |
将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高
的最小值为 ( )
A.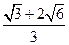 |
B.2+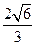 |
C.4+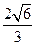 |
D.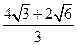 |
若钝角三角形三内角的度数成等差数列,且最大边长与最小边长的比值为m,则
m的范围是( )
| A.(1,2) | B.(2, +∞) +∞) |
C.[3,+∞ |
D.(3,+∞) |
如图,在半径为r 的圆内作内接正六边形,再 作正六边形的内切圆,又在此内切
作正六边形的内切圆,又在此内切
圆内作内接正六边形,如此无限继续下去,设 为前n个圆的面积之和,则
为前n个圆的面积之和,则
 =( )
=( )
A.2 |
B.  |
C.4 |
D.6 |
已知等比数列{ }中,各项都是正数,且
}中,各项都是正数,且 ,
, 成等差数列,则
成等差数列,则
( )
A. |
B. |
C. |
D. |
一给定函数 的图象在下列图中,并且对任意
的图象在下列图中,并且对任意 ,由关系式
,由关系式 得到的数列
得到的数列 满足
满足 ,则该函数的图象是( )
,则该函数的图象是( )
已知︱ ︱=1,︱
︱=1,︱ ︱=
︱= ,
, =0,点C在∠AOB内,且∠AOC=30°,
=0,点C在∠AOB内,且∠AOC=30°,
设 =m
=m +n
+n (m、n∈R),则
(m、n∈R),则 等于 ( )
等于 ( )
A. |
B.3 | C. |
D. |