定义一种新运算：a⊗b=
，已知函数f（x）=（1+
）⊗3log2（x+1），若方程f（x）﹣k=0恰有两个不相等的实根，则实数k的取值范围为（ ）
| A．（﹣∞，3） |
| B．（1，3） |
| C．（﹣∞，﹣3）∪（1，3） |
| D．（﹣∞，﹣3）∪（0，3） |
一支人数是5的倍数且不少于1000人的游行队伍，若按每横排4人编队，最后差3人；若按每横排3人编队，最后差2人；若按每横排2人编队，最后差1人．则这只游行队伍的最少人数是（ ）
| A．1025 | B．1035 | C．1045 | D．1055 |
从1开始的自然数按如图所示的规则排列，现有一个三角形框架在图中上下或左右移动，使每次恰有九个数在此三角形内，则这九个数的和可以为（ ）
| A．2097 | B．1553 | C．1517 | D．2111 |
若数列{an}满足：存在正整数T，对于任意正整数n都有an+T=an成立，则称数列{an}为周期数列，周期为T．已知数列{an}满足a1=m（m＞0），an+1=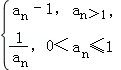
则下列结论中错误的是（ ）
A．若m= ，则a5=3 |
| B．若a3=2，则m可以取3个不同的值 |
C．若m= ，则数列{an}是周期为3的数列 |
| D．∃m∈Q且m≥2，数列{an}是周期数列 |
已知函数f（x）定义域为D，若∀a，b，c∈D，f（a），f（b），f（c）都是某一三角形的三边，则称f（x）为定义在D上的“保三角形函数”，以下说法正确的个数有（ ）
①f（x）=1（x∈R）不是R上的“保三角形函数”
②若定义在R上的函数f（x）的值域为[
，2]，则f（x）一定是R上的“保三角形函数”
③f（x）=
是其定义域上的“保三角形函数”
④当t＞1时，函数f（x）=ex+t一定是[0，1]上的“保三角形函数”
| A．1个 | B．2个 | C．3个 | D．4个 |
在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
（1）对任意a∈R，a*0=a；
（2）对任意a，b∈R，a*b=ab+（a*0）+（b*0）．
则函数f（x）=（ex）*
的最小值为（ ）
| A．2 | B．3 | C．6 | D．8 |
两旅客坐火车外出旅游，希望座位连在一起，且有一个靠窗，已知火车上的座位的排法如图所示，则下列座位号码符合要求的应当是（ ）
| A．48，49 | B．62，63 | C．75，76 | D．84，85 |
对于任意实数a，b，c，定义Г（a，b，c）满足Г（a，b，c）=Г（b，c，a）=Г（c，a，b）关系式，则称Г（a，b，c）具有轮换对称关系，给出如下四个式子：
①Г（a，b，c）=a+b+c；
②Г（a，b，c）=a2﹣b2+c2；
③Г（x，y，z）=xy+yz+zx；
④Г（A，B，C）=2sinAsinBsinC+cos（
﹣A）sin（π﹣B）sinC（A、B、C是△ABC的内角）
其中具有轮换对称关系的个数是（ ）
A.1 B.2 C.3 D.4
一个机器人每一秒钟前进或后退一步，程序设计师让机器人以前进3步，然后再后退2步的规律移动．如果将机器人放在数轴的原点，面向正的方向，以1步的距离为1个单位长度．令P（n）表示第n秒时机器人所在位置的坐标，且记P（0）=0，则下列结论中错误的是（ ）
| A．P（3）=3 | B．P（5）=1 | C．P（2003）＞P（2005） | D．P（2003）＜P（2005） |
对于正实数α，Mα为满足下述条件的函数f（x）构成的集合：∀x1，x2∈R且x2＞x1，有﹣α（x2﹣x1）＜f（x2）﹣f（x1）＜α（x2﹣x1）．下列结论中正确的是（ ）
| A．若f（x）∈Mα1，g（x）Mα2，则f（x）•g（x）∈Mα1•α2 |
B．若f（x）∈Mα1，g（x）∈Mα2，且g（x）≠0，则 |
| C．若f（x）∈Mα1，g（x）∈Mα2，则f（x）+g（x）∈Mα1+α2 |
| D．若f（x）∈Mα1，g（x）∈Mα2，且α1＞α2，则f（x）﹣g（x）∈Mα1﹣α2 |
从1开始的自然数按如图所示的规则排列，现有一个三角形框架在图中上下或左右移动，使每次恰有九个数在此三角形内，则这九个数的和可以为（ ）
| A．2097 | B．2112 | C．2012 | D．2090 |
设△ABC的三边长分别为a、b、c，△ABC的面积为S，内切圆半径为r，则
，类比这个结论可知：四面体S﹣ABC的四个面的面积分别为S1、S2、S3、S4，内切球半径为r，四面体S﹣ABC的体积为V，则r=（ ）
A． |
B． |
C． |
D． |
学生的语文、数学成绩均被评定为三个等级，依次为“优秀”“合格”“不合格”．若学生甲的语文、数学成绩都不低于学生乙，且其中至少有一门成绩高于乙，则称“学生甲比学生乙成绩好”．如果一组学生中没有哪位学生比另一位学生成绩好，并且不存在语文成绩相同、数学成绩也相同的两位学生，则这一组学生最多有（ ）
| A．2人 | B．3人 | C．4人 | D．5人 |
加工爆米花时，爆开且不糊的粒数占加工总粒数的百分比称为“可食用率”，在特定条件下，可食用率p与加工时间t（单位：分钟）满足函数关系p=at2+bt+c（a，b，c是常数），如图记录了三次实验的数据，根据上述函数模型和实验数据，可以得到最佳加工时间为（ ）
| A．3.50分钟 | B．3.75分钟 | C．4.00分钟 | D．4.25分钟 |
粤公网安备 44130202000953号
}+{
}+{
}+…+{
}=（ ）