有人从“若a<b,则2a< <2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)<
<2b”中找到灵感引入一个新概念,设F(x)=x2,f(x)=2x,于是有f(a)< <f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
<f(b),此时称F(x)为甲函数,f(x)为乙函数,下面命题正确的是( )
| A.若f(x)=3x2+2x则F(x)=x3+x2+C,C为常数 |
| B.若f(x)=cosx,则F(x)=sinx+C,C为常数 |
| C.若f(x)=x2+1,则F(x)为奇函数 |
| D.若f(x)=ex,则F(2)<F(3)<F(5) |
已知为自然对数的底数,设函数
,则()
| A. |
当
|
| B. |
当
|
| C. |
当
|
| D. |
当
|
下面说法正确的是
A.若 在 在 处存在极限,则 处存在极限,则 在 在 处连续 处连续 |
B.若 在 在 处无定义,则 处无定义,则 在 在 处无极限 处无极限 |
C.若 在 在 处连续,则 处连续,则 在 在 处存在极限 处存在极限 |
D.若 在 在 处连续,则 处连续,则 在 在 处可导 处可导 |
曲线 在点
在点 处的切线方程为( )
处的切线方程为( )
A. |
B. |
C. |
D. |
已知函数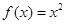 的图象在点
的图象在点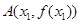 与点
与点 处的切线互相垂直,
处的切线互相垂直,
并交于点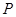 ,则点
,则点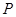 的坐标可能是( )
的坐标可能是( )
A.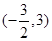 |
B. |
C.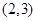 |
D.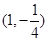 |
某汽车启动阶段的位移函数为s(t)=2t3﹣5t2,则汽车在t=2时的瞬时速度为( )
| A.10 | B.14 | C.4 | D.6 |
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x+y+3=0垂直,若数列{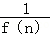 }的前n项和为Sn,则S2011的值为( )
}的前n项和为Sn,则S2011的值为( )
A.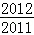 |
B.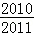 |
C.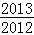 |
D.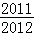 |
已知曲线 的一条切线的斜率为
的一条切线的斜率为 ,则切点的横坐标为( )
,则切点的横坐标为( )
| A.3 | B.2 | C.1 | D. |
曲线y=e2x在点(0,1)处的切线方程为( ).
A.y= x+1 x+1 |
B.y=﹣2x+1 | C.y=2x﹣1 | D.y=2x+1 |
曲线y=-x3+3x2在点(1,2)处的切线方程为 ( ).
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |