曲线y=-x3+3x2在点(1,2)处的切线方程为 ( ).
| A.y=3x-1 | B.y=-3x+5 |
| C.y=3x+5 | D.y=2x |
已知函数y=f(x)的图象如图,则f′(xA)与f′(xB)的大小关系是( ).
| A.f′(xA)>f′(xB) | B.f′(xA)<f′(xB) |
| C.f′(xA)=f′(xB) | D.不能确定 |
过曲线C: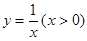 上一点
上一点 作曲线C的切线,若切线的斜率为-4,则
作曲线C的切线,若切线的斜率为-4,则 等于( )
等于( )
| A.2 | B. |
C.4 | D.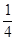 |
抛物线y=x2在点P处的切线与直线2x-y+4=0平行,求点P的坐标及切线方程.
已知函数 在
在 上可导,且
上可导,且 ,则函数
,则函数 的解析式为( )
的解析式为( )
A. |
B. |
C. |
D. |
已知函数 ∈R).
∈R).
(1)若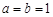 ,求
,求 点(
点(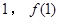 )处的切线方程;
)处的切线方程;
(2)设a≤0,求 的单调区间;
的单调区间;
(3)设a<0,且对任意的 ,
, ≤
≤ ,试比较
,试比较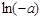 与
与 的大小.
的大小.