已知 为非零实数,函数
为非零实数,函数
(Ⅰ)求函数 的单调区间
的单调区间
(Ⅱ)若直线 与
与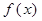 和
和 的图像都相切,则称直线
的图像都相切,则称直线 是
是 和
和 的公切线,已知函数
的公切线,已知函数 和
和 有两条公切线
有两条公切线
(1)求 的取值范围
的取值范围
(2)若 分别为直线
分别为直线 与
与 图像的两个切点的横坐标,求证:
图像的两个切点的横坐标,求证:
已知函数 (其中
(其中 ,
, ),函数
),函数 的导函数为
的导函数为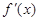 ,且
,且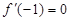 .
.
(Ⅰ)若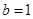 ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程;
(Ⅱ)若函数 在区间
在区间 上的最小值为
上的最小值为 ,求
,求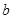 的值.
的值.
设函数 ,
,
(1)若函数 在
在 处与直线
处与直线 相切;
相切;
①求实数 ,
, 的值;②求函数
的值;②求函数 上的最大值;
上的最大值;
(2)当 时,若不等式
时,若不等式 对所有的
对所有的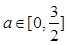 ,
,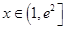 都成立,求实数
都成立,求实数 的取值范围.
的取值范围.
设函数 ,则下列结论正确的是()
,则下列结论正确的是()
A.函数 上单调递增 上单调递增 |
B.函数 上单调递减 上单调递减 |
C.若 ,则函数 ,则函数 的图象在点 的图象在点 处的切线方程为y=10 处的切线方程为y=10 |
D.若b=0,则函数 的图象与直线y=10只有一个公共点 的图象与直线y=10只有一个公共点 |