高中数学表面展开图填空题

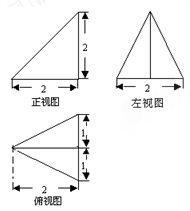
已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是    .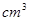

如图，正方体ABCD—A₁B₁C₁D₁，

则下列四个命题：
①P在直线BC₁上运动时，三棱锥A—D₁PC的体积不变；
②P在直线BC₁上运动时，直线AP与平面ACD₁所成角的大小不变；
③P在直线BC₁上运动时，二面角P—AD₁—C的大小不变；
④M是平面A₁B₁C₁D₁上到点D和C₁距离相等的点，则M点的轨迹是过D₁点的直线D₁A₁．
其中真命题的编号是    ．

在三棱锥P-ABC中侧棱PA，PB，PC两两垂直，Q为底面△ABC内一点，若点Q到三个侧面的距离分别为3,4,5，则过点P和Q的所有球中，表面积最小的球的表面积为          .

利用一个球体毛坯切削后得到一个四棱锥,其中底面四边形是边长为的正方形，，且平面,则球体毛坯体积的最小值应为       ．

如图，在棱长为2的正方体ABCD A₁B₁C₁D₁中，E，F分别是棱AB，BC中点，则三棱锥B B₁EF的体积为________．

三棱锥中，平面，为侧棱上一点，它的正视图和侧视图 （如下图所示），则与平面所成角的大小为__     _；三棱锥的体积为 __      _．

在三棱锥中，，，，二面角的余弦值是，若都在同一球面上，则该球的表面积是        .

已知直三棱柱中，，侧面的面积为，则直三棱柱
外接球表面积的最小值为         ．

如图，在正方体中，点在面对角线上运动，给出下列四个命题：

①∥平面；    ②；
③平面⊥平面；④三棱锥的体积不变.
则其中所有正确的命题的序号是     ．

椭圆绕轴旋转一周所得的旋转体的体积为     ．

已知点P，A，B，C，D是球O表面上的点，PA⊥平面ABCD，四边形ABCD是边长为的正方形．若，则△OAB的面积为_______．

已知三棱柱的侧棱垂直于底面，各顶点都在同一球面上，若该棱柱的体积为，，，则此球的表面积等于__________．

如图，在棱柱的侧棱上各有一个动点，且满足，是棱上的动点，则的最大值是          ．

如图，在长方体中，，沿该长方体对角面将其截成两部分，并将它们再拼成一个新的四棱柱，那么这个四棱柱表面积的最大值为___________．

如图水平放置的三棱柱的侧棱长为1，且侧棱平面，主视图是边长为1的正方形，俯视图为一个等边三角形，则该三棱柱的左视图面积为________.