如图,半径为R的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是。
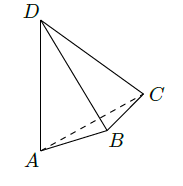
如图, 与 是四面体 中互相垂直的棱, . 若 ,且 ,其中 、 为常数,则四面体 的体积的最大值是.
已知一个三棱锥的三视图如图所示,其中主视图、俯视图是全等的等腰直角三角形,则该三棱锥的外接球体积为.
如图是一个长方体ABCD-A1B1C1D1截去一个角后的多面体的三视图,在这个多面体
中,AB=4,BC=6,CC1=3.则这个多面体的体积为.
已知三棱锥O-ABC中,OA、OB、OC两两互相垂直,OC=1,OA=x, OB=y,若x+y=4,则已知三棱锥O-ABC体积的最大值是.
把边长为 的正方形
的正方形 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面 ,形成三棱锥
,形成三棱锥 的正视图与俯视图如右图所示,则侧视图的面积为 。
的正视图与俯视图如右图所示,则侧视图的面积为 。
下图都是由边长为1的正方体叠成的图形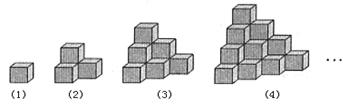
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位,第(4)个图形的表面积是60个平方单位.依此规律,则第(8)个图形的表面积是▲个平方单位.
现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形生重叠部分的面积恒为 ,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为;
,类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为;
如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点E, F,且
上有两个动点E, F,且 ,则四面体
,则四面体 的体积
的体积
|

正三棱锥S-ABC中,M、N分别是SC.BC中点,且MN⊥AM,若SA=2 .则正三棱锥S - ABC的外接球的体积为。
.则正三棱锥S - ABC的外接球的体积为。