如图,正方体 的棱长为1,线段
的棱长为1,线段 上有两个动点
上有两个动点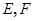 ,且
,且 ,则下列结论中正确的有 .(填写你认为正确的序号)
,则下列结论中正确的有 .(填写你认为正确的序号)
① ;
;
② ;
;
③若 为
为 上的一动点,则三棱锥
上的一动点,则三棱锥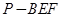 的体积为定值;
的体积为定值;
④在空间与直线 都相交的直线只有1条。
都相交的直线只有1条。
已知点A、B、C、D均在球O上,AB=BC= ,AC=3,若三棱锥D﹣ABC体积的最大值为
,AC=3,若三棱锥D﹣ABC体积的最大值为 ,则球O的表面积为()
,则球O的表面积为()
A.36πB.16π C.12π D. π
π
如图,已知三棱柱ABC﹣A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱CC1到点A1的最短路线长为2 ,设这条最短路线与交于点D.
,设这条最短路线与交于点D.
(1)求三棱柱ABC﹣A1B1C1的棱长;
(2)求四棱锥A1﹣BCC1B1的体积;
(3)在平面A1BD内是否存在过点D的直线与平面ABC平行?并说明理由.
将正方形ABCD沿对角线BD折叠成一个四面体ABCD,当该四面体的体积最大时,直线AB与CD所成的角为()
| A.90° | B.60° | C.45° | D.30° |
如图,将矩形ABCD沿对角线BD把△ABD折起,使A点移到A1点,且A1在平面BCD上的射影O恰好在CD上.

(Ⅰ)求证:BC⊥A1D;
(Ⅱ)求证:平面A1CD⊥平面A1BC;
(Ⅲ)若AB=10,BC=6,求三棱锥A1﹣BCD的体积.
已知四面体P-ABC的外接球的球心O在AB上,且PO⊥平面ABC, , 若四面体P-ABC的体积为
, 若四面体P-ABC的体积为 ,则该球的体积为()
,则该球的体积为()
A. |
B. |
C. |
D. |