高中数学表面展开图试题

如图，一个圆锥的底面半径为2cm，高为6cm，其中有一个高为xcm的内接圆柱．

（1）试用x表示圆柱的侧面积；
（2）当x为何值时，圆柱的侧面积最大．

某几何体的三视图如下图所示，则该几何体中，面积最大的侧面的面积为（）

A．

B．

C．

D．

如图：直三棱柱ABC﹣A′B′C′的体积为V，点P、Q分别在侧棱AA′和CC′上，AP=C′Q，则四棱锥B﹣APQC的体积为 ．

设一个正方体与底面边长为，侧棱长为的正四棱锥的体积相等，则该正方体的棱长为 ．

如果轴截面为正方形的圆柱的侧面积是4π，那么圆柱的体积等于（）

A．π

B．2π

C．4π

D．8π

如图，平面平面，四边形是直角梯形，，，，是等腰直角三角形，，分别是的中点.

（1）求证：平面；
（2）求三棱锥的体积.

在底面半径为2，母线长为4的圆锥中内有一个高为的圆柱．
（1）求：圆柱表面积的最大值；
（2）在（1）的条件下，求该圆柱外接球的表面积和体积．

已知各顶点都在一个球面上的正四棱柱的高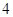为，体积为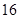，则球的表面积是（）

A．

B．

C．

D．

某四棱锥的三视图如图所示，该四棱锥的体积是（）

A．32

B．

C．48

D．

将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（）

A．4π

B．3π

C．2π

D．π

一个几何体的三视图如图，则该几何体的体积是（）

A．+8

B．7+4

C．+8

D．+4

如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点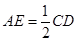，，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示。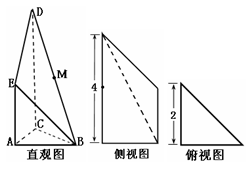

（Ⅰ）求出该几何体的体积；
（Ⅱ）试问在边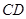上是否存在点N，使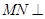平面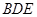？ 若存在，确定点N的位置(不需证明)；若不存在，请说明理由。

某几何体三视图如下，图中三个等腰三角形的直角边长都是，该几何体的体积为（）

A．	B．
C．	D．

正方体的棱长为，则其外接球的表面积为（）

A．

B．

C．

D．

设一个圆锥的侧面展开图是半径为的半圆，则此圆锥的体积为 ．