如图,三棱锥A-BCD中,AB 平面BCD,BC
平面BCD,BC CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为()
CD,若AB=BC=CD=2,则该三棱锥的侧视图(投影线平行于BD)的面积为()
A. B.2 C.
B.2 C. D.
D.
如图,一个空间几何体的正视图(或称主视图)、侧视图(或称左视图)、俯视图均为全等的等腰直角三角形,如果直角三角形的斜边长为 ,那么这个几何体的体积为
,那么这个几何体的体积为
| A.1 | B. |
C. |
D. |
已知三棱锥 的所有顶点都在球
的所有顶点都在球 的球面上,
的球面上, 是边长为
是边长为 的正三角形,
的正三角形,  为球
为球 的直径,且
的直径,且 ;则此棱锥的体积为()
;则此棱锥的体积为()
A. |
B. |
C. |
D. |
如图是一个几何体的三视图,其中正视图和侧视图都是一个两底长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是
| A.6π | B.12π | C.18π | D.24π |
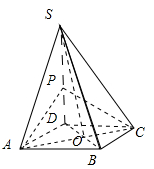
(本小题12分)如图4,四棱锥 中,底面
中,底面 是菱形,其对角线的交点为
是菱形,其对角线的交点为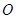 ,且
,且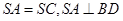 .
.
(1)求证: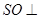 平面
平面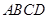 ;
;
(2)设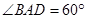 ,
,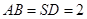 ,
,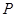 是侧棱
是侧棱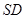 上的一点,且
上的一点,且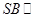 平面
平面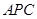 ,求三棱锥
,求三棱锥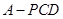 的体积.
的体积.
一个长方体被一个平面截去一部分后所剩几何体的三视图如图所示(单位: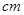 ),则该几何体的体积为()
),则该几何体的体积为()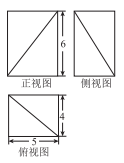
A.120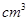 |
B.80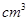 |
C.100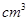 |
D.60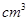 |
如图,三棱柱 中,侧棱
中,侧棱 平面
平面 ,
, 为等腰直角三角形,
为等腰直角三角形,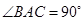 ,且
,且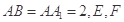 分别是
分别是 的中点.
的中点.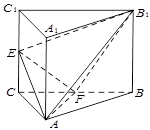
(1)求证: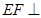 平面
平面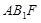 ;
;
(2)求三棱锥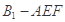 的体积.
的体积.
(3)若点 是
是 上一点,求
上一点,求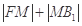 的最小值.
的最小值.
如图是一个无盖器皿的三视图,正视图、侧视图和俯视图中的正方形边长为2,正视图、侧视图中的虚线都是半圆,则该器皿的表面积是( )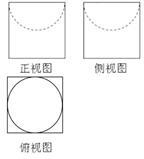
A. |
B.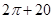 |
C. |
D.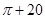 |