设 为两个不同平面,m、 n为两条不同的直线,且
为两个不同平面,m、 n为两条不同的直线,且 有两个命题:
有两个命题:
P:若m∥n,则 ∥β;q:若m⊥β, 则α⊥β. 那么( )
∥β;q:若m⊥β, 则α⊥β. 那么( )
| A.“p或q”是假命题 | B.“p且q”是真命题 |
| C.“非p或q”是假命题 | D.“非p且q”是真命题 |
已知命题p:函数 在(0,1)内恰有一个零点;命题q:函数
在(0,1)内恰有一个零点;命题q:函数 在
在 上是减函数,若p且
上是减函数,若p且 为真命题,则实数a的取值范围是( )
为真命题,则实数a的取值范围是( )
A. |
B.a≤2 | C.1<a≤2 | D.a≤l或a>2 |
设 为两个不同平面,m、 n为两条不同的直线,且
为两个不同平面,m、 n为两条不同的直线,且 有两个命题:
有两个命题:
P:若m∥n,则 ∥β;q:若m⊥β, 则α⊥β. 那么( )
∥β;q:若m⊥β, 则α⊥β. 那么( )
| A.“p或q”是假命题 | B.“p且q”是真命题 |
| C.“非p或q”是假命题 | D.“非p且q”是真命题 |
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x∈R”,x2+2ax+2-a=0,若命题“p∧q”是真命题,则实数a的取值范围是( )
| A.a≤-2或a=1 | B.a≤-2或1≤a≤2 |
| C.a≥1 | D.-2≤a≤1 |
已知命题p:“∀x∈[1,2],x2-a≥0”,命题q:“∃x∈R”,x2+2ax+2-a=0,若命题“p∧q”是真命题,则实数a的取值范围是( )
| A.a≤-2或a=1 | B.a≤-2或1≤a≤2 |
| C.a≥1 | D.-2≤a≤1 |
下列说法:
①命题“存在 ” 的否定是“对任意的
” 的否定是“对任意的 ”;
”;
②关于 的不等式
的不等式 恒成立,则
恒成立,则 的取值范围是
的取值范围是 ;
;
③函数 为奇函数的充要条件是
为奇函数的充要条件是 ;其中正确的个数是( )
;其中正确的个数是( )
| A.3 | B.2 | C.1 | D.0 |
下列说法中正确的是( )
A.“ ”是“ ”是“ ”必要条件 ”必要条件 |
B.命题“ , , ”的否定是“ ”的否定是“ , , ” ” |
C. ,使函数 ,使函数 是奇函数 是奇函数 |
D.设 , , 是简单命题,若 是简单命题,若 是真命题,则 是真命题,则 也是真命题 也是真命题 |
下列说法中正确的是( )
A.“ ”是“ ”是“ ”必要条件 ”必要条件 |
B.命题“ , , ”的否定是“ ”的否定是“ , , ” ” |
C. ,使函数 ,使函数 是奇函数 是奇函数 |
D.设 , , 是简单命题,若 是简单命题,若 是真命题,则 是真命题,则 也是真命题 也是真命题 |
已知命题p:∀x∈(0, ),3x>2x,命题q:∃x∈(
),3x>2x,命题q:∃x∈( ,0),
,0), ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
| A.p∧q | B.(¬p)∧q | C.(¬p)∧(¬q) | D.p∧(¬q) |
已知 ,命题
,命题 为
为 ,命题
,命题 为
为 .则命题
.则命题 成立是命题
成立是命题 成立的 ( ).
成立的 ( ).
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.非充分非必要条件 |
命题“若 ,则
,则 ”的逆否命题是( )
”的逆否命题是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 或 或 ,则 ,则 |
D.若 或 或 ,则 ,则 |
已知命题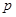 “任意
“任意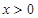 ,
,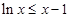 ”,则
”,则 为( )
为( )
A.存在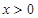 , ,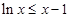 |
B.存在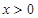 , ,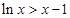 |
C.任意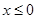 , ,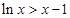 |
D.任意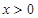 , ,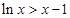 |