下列四个命题: ,
, ”是全称命题;
”是全称命题;
命题“ ,
, ”的否定是“
”的否定是“ ,使
,使 ”;
”;
若 ,则
,则 ;
;
若 为假命题,则
为假命题,则 、
、 均为假命题.
均为假命题.
其中真命题的序号是( )
| A.①② | B.①④ | C.②④ | D.①②③④ |
已知命题 :函数
:函数 在
在 内单调递减;
内单调递减; :曲线
:曲线 与
与 轴没有交点.如果“
轴没有交点.如果“ 或
或 ”是真命题,“
”是真命题,“ 且
且 ”是假命题,则实数
”是假命题,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
原命题为"若,
,则
为递减数列",关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是()
| A. | 真,真,真 | B. | 假,假,真 | C. | 真,真,假 | D. | 假,假,假 |
已知命题对任意
,总有
;
是方程
的根
则下列命题为真命题的是()
| A. |
|
B. |
|
C. |
|
D. |
|
已知命题.在命题
中,真命题是()
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
下列命题:①已知平面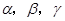 满足
满足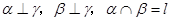 则
则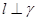 .
.
②E,F,G,H是空间四边形ABCD各边AB,BC,CD,DA的中点,若对角线BD=2,AC=4,则
③过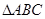 所在平面
所在平面 外一点P,作
外一点P,作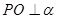 ,垂足为O,连接PA,PB,PC,若
,垂足为O,连接PA,PB,PC,若 ,则点O是
,则点O是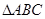 的垂心
的垂心
其中正确命题的序号是 。
已知命题p:“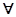 x∈[1,2],x2-a≥0”,命题q:“
x∈[1,2],x2-a≥0”,命题q:“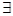 x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
x∈R使x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
A.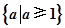 |
B. |
C. |
D.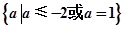 |
下列四个命题:
①利用计算机产生0~1之间的均匀随机数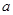 ,则事件“
,则事件“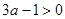 ”发生的概率为
”发生的概率为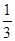 ;
;
②“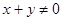 ”是“
”是“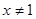 或
或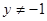 ”的充分不必要条件;
”的充分不必要条件;
③命题“在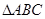 中,若
中,若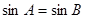 ,则
,则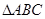 为等腰三角形”的否命题为真命题;
为等腰三角形”的否命题为真命题;
④如果平面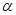 不垂直于平面
不垂直于平面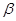 ,那么平面
,那么平面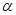 内一定不存在直线垂直于平面
内一定不存在直线垂直于平面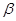 。
。
其中说法正确的个数是( )
| A.0个 | B.1个 | C.2个 | D.3个 |
下列四个命题中,真命题的序号有 .(写出所有真命题的序号)
①若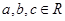 ,则“
,则“ ”是“
”是“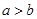 ”成立的充分不必要条件;
”成立的充分不必要条件;
②命题“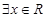 使得
使得 ”的否定是“
”的否定是“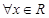 均有
均有 ”;
”;
③命题“若 ,则
,则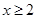 或
或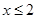 ”的否命题是“若
”的否命题是“若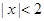 ,则
,则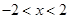 ”;
”;
④函数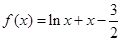 在区间
在区间 上有且仅有一个零点.
上有且仅有一个零点.
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p∨q”是假命题,求实数a的取值范围.
给出下面四个命题:
p1:∃x∈(0,+∞),( )x<(
)x<( )x;
)x;
p2:∃x∈(0,1), x>
x> x;
x;
p3:∀x∈(0,+∞),( )x>
)x> x;
x;
p4:∀x∈(0, ),(
),( )x<
)x< x.
x.
其中的真命题是( )
| A.p1,p3 | B.p1,p4 | C.p2,p3 | D.p2,p4 |
已知命题p:∀x∈(1,+∞),log2x<log3x;命题q:∃x∈(0,+∞),2-x=lnx.则下列命题中为真命题的是( )
| A.p∧q | B.( p)∧q p)∧q |
C.p∧( q) q) |
D.( p)∧( p)∧( q) q) |
已知命题P:函数y=loga(1-2x)在定义域上单调递增;命题Q:不等式(a-2)x2+2(a-2)x-4<0对任意实数x恒成立.若P∨Q是真命题,求实数a的取值范围.