某微机培训机构打算购进一批微机桌和鼠标垫 ,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这
,市场价微机桌每张为150元,鼠标垫每个为5元,该培训机构老板联系了两家商场甲和乙,由于用货量大,这 两家商场都给出了优惠条件
两家商场都给出了优惠条件
商场甲:买一赠一,买一张微机桌,赠一个鼠标垫
商场乙:打折,按总价的95%收款
该培训机构需要微机桌 60张,鼠标垫
60张,鼠标垫 个(
个( ),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?
),如果两种商品只能在一家购买,请你帮助该培训机构老板选择在哪一家商场买更省钱?
(本小题12分)
已知函数f (x2-3) = lg ,
,
(1) f(x)的 定义域;
定义域;
(2) 判断f(x)的奇偶性;
(3) 若f [ ] = lgx,求
] = lgx,求 的值。
的值。
(本小题12分)
某企业为适应市场需求,准备投入资金16万元生产W和R型两种产品。经市场预测,生产W型产品所获利润 (万元)与投入资金
(万元)与投入资金 (万元)成正比例关系,且当投入资金为6万元时,可获利润1.5
(万元)成正比例关系,且当投入资金为6万元时,可获利润1.5 万元。生产R型产品所获利润
万元。生产R型产品所获利润 (万元)与投入资金
(万元)与投入资金 (
( 万元)满足关系
万元)满足关系 ,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
,为获得最大总利润,问生产W、R型产品各应投入资金多少万元?获得的最大总利润是多少?
(本小题满分12分)
已知定义域为 的函数
的函数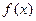 满足:①
满足:①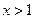 时,
时,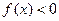 ;②
;②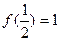 ③对任意的正实数
③对任意的正实数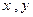 ,都有
,都有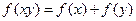
(1)求证: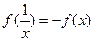 ;(2)求证:
;(2)求证: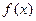 在定义域内为减函数;
在定义域内为减函数;
(3)求不等式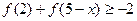 的解集.
的解集.
(14分)已知函数 的图象过原点,且关于点(-1,1)成中心对称.(1)求函数
的图象过原点,且关于点(-1,1)成中心对称.(1)求函数 的解析式;(2) 若数列
的解析式;(2) 若数列 (nÎN*)满足:
(nÎN*)满足: ,求数列
,求数列 的通项公式
的通项公式 .
.
已知函数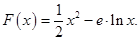
(I)求函数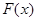 的极值;
的极值;
(II)对于函数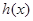 和
和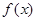 定义域内的任意实数
定义域内的任意实数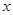 ,若存在常数
,若存在常数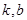 ,使得不等式
,使得不等式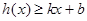 和
和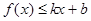 都成立,则称直线
都成立,则称直线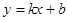 是函数
是函数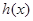 和
和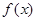 的“分界线”.
的“分界线”.
设函数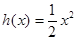 ,
,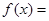
 ,试问函数
,试问函数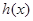 和
和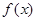 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
已知某公司生产某品牌服装的年固定成本为10万元,每生产千件需另投入2.7万元,设该公司年内共生产该品牌服装千件并全部销售完,每千件的销售收入为 万元,且
万元,且 .
.
(1)写出年利润 (万元)关于年产品(千件)的函数解析式;
(万元)关于年产品(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
(注:年利润=年销售收入-年总成本)
(本题满分16分)
已知函数 ,其中
,其中 ,
,
(1)当 时,把函数
时,把函数 写成分段函数的形式;
写成分段函数的形式;
(2)当 时,求
时,求 在区间
在区间 上的最值;
上的最值;
(3)设 ,函数
,函数 在
在 上既有最大值又有最小值,请分别求出
上既有最大值又有最小值,请分别求出 的取值范围(用
的取值范围(用 表示).
表示).