如图中, 为某次考试三个评阅人对同一道题的独立评分, 为该题的最终得分,当 时 等于()
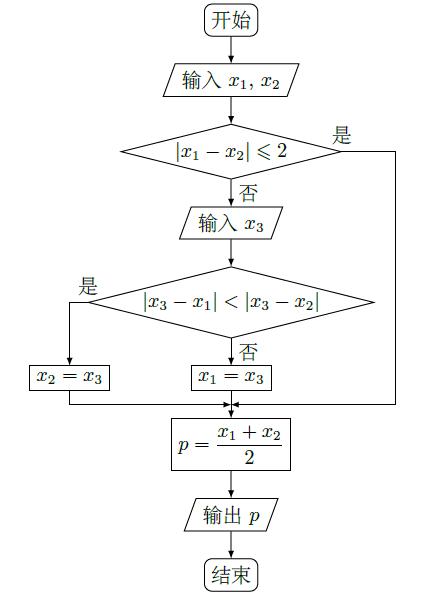
| A. | 11 | B. | 10 | C. | 8 | D. | 7 |
设
,已知函数
.
(Ⅰ)当
时,讨论函数
的单调性;
(Ⅱ)当
时,称
为
关于
的加权平均数.
(1)判断
是否成等比数列,并证明
;
(2)
的几何平均数记为
.称
为
的调和平均数,记为
.若
,求
的取值范围.
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
| A.y=cos 2x,x∈R |
| B.y=log2|x|,x∈R且x≠0 |
C.y=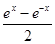 ,x∈R ,x∈R |
| D.y=x3+1,x∈R |