已知函数 (
( ),该函数所表示的曲线上的一个最高点为
),该函数所表示的曲线上的一个最高点为 ,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
,由此最高点到相邻的最低点间曲线与x轴交于点(6,0)。
(1)求 函数解析式;
函数解析式;
(2)求函数 的单调区间;
的单调区间;
(3)若 ,求
,求 的值域。
的值域。
已知 ,
, 。
。
(1)求 的振幅,最小正周期,对称轴,对称中心。
的振幅,最小正周期,对称轴,对称中心。
(2)说明 是由余弦曲线经过怎样变换得到。
是由余弦曲线经过怎样变换得到。
已知 为坐标原点,对于函数
为坐标原点,对于函数 ,称向量
,称向量 为函数
为函数 的伴随向量,同时称函数
的伴随向量,同时称函数 为向量
为向量 的伴随函数.
的伴随函数.
(Ⅰ)设函数 ,试求
,试求 的伴随向量
的伴随向量 的模;
的模;
(Ⅱ)记 的伴随函数为
的伴随函数为 ,求使得关于
,求使得关于 的方程
的方程 在
在 内恒有两个不相等实数解的实数的取值范围.
内恒有两个不相等实数解的实数的取值范围.
函数 (
( )的部分图像如图所示.
)的部分图像如图所示.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ) 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
,
其中 ,且
,且 ,求角
,求角 的大小.
的大小.
已知函数 .
.
(1)求 的最小正周期;
的最小正周期;
(2)在 中,
中, 分别是
分别是 A、
A、 B、
B、 C的对边,若
C的对边,若 ,
, ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
已知向量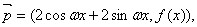
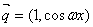 ,
,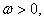
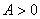 且
且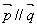 ,
,
函数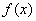 图象上相邻两条对称轴之间的距离是
图象上相邻两条对称轴之间的距离是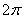 ,
,
(1)求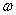 值;
值;
(2)求函数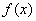 的单调递减区间;
的单调递减区间;
(3)设函数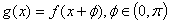 ,若
,若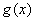 为偶函数,,求
为偶函数,,求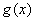 的最大值及
的最大值及
相应的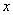 值
值
已知函数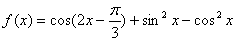 ,
, 
(1)求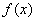 的对称轴方程;
的对称轴方程;
(2)用“五点法”画出函数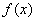 在一个周期内的简图;
在一个周期内的简图;
(3)若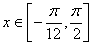 ,设函数
,设函数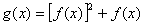 ,求
,求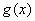 的值域。
的值域。
已知向量 =(
=( sin2x+2,cosx),
sin2x+2,cosx), =(1,2cosx),设函数f(x)=
=(1,2cosx),设函数f(x)=  ·
· .
.
(I)求f(x)的最小正周期与单调递增区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,若A= ,b=f(
,b=f( ),ΔABC的面积为
),ΔABC的面积为 ,求a的值
,求a的值
已知函数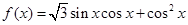 .
.
(1)写出函数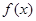 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(2)若函数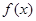 的图象关于直线
的图象关于直线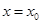 对称,且
对称,且 ,求
,求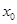 的值.
的值.