高中数学多面角及多面角的性质选择题

同时具有性质：（1）最小正周期是；（2）图象关于直线对称；（3）在上是增函数的一个函数是（    ）

A．	B．
C．	D．

同时具有性质：（1）最小正周期是；（2）图象关于直线对称；（3）在上是增函数的一个函数是（    ）

A．	B．
C．	D．

将函数的图象向右平移个单位后得到函数，则具有性质（  ）

A．最大值为，图象关于直线对称

B．在上单调递增，为奇函数

C．在上单调递增，为偶函数

D．周期为，图象关于点对称

把函数的图象向右平移，得到函数的图象，则函数为（  ）

A．周期为的奇函数	B．周期为的偶函数
C．周期为的奇函数	D．周期为的偶函数

【改编】函数的值域为（   ）

A．

B．

C．

D．

【改编】若函数在区间上单调递增，在区间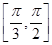上单调递减，则关于说法正确的是（   ）

A．对称中心是	B．对称轴是
C．对称中心是	D．对称轴是

【改编】为了得到的图象，只需将的图象  

A．把各点的横坐标缩短到原来的倍，再向右平移个长度单位

B．把各点的横坐标缩短到原来的倍，再向左平移个长度单位

C．把各点的横坐标缩短到原来的倍，再向右平移个长度单位

D．把各点的横坐标缩短到原来的倍，再向左平移个长度单位

【改编】函数（其中）的图象如图所示，为了得到的图象，只需把的图象上所有点（    ）个单位长度．

A．向右平移

B．向右平移

C．向左平移

D．向左平移

将函数的图像向左平移个单位后的图像关于原点对称，则函数在上的最小值为
                                           

将函数的图像向左平移个单位后的图像关于原点对称，则函数在上的最小值为
                                           

设函数，则下列结论正确的是（   ）
①的图象关于直线对称；  
②的图象关于点对称；
③的图象向左平移个单位，得到一个偶函数的图象；
④的最小正周期为，且在上为增函数．

A．①③

B．②④

C．①③④

D．③

函数的图象是由函数的图象向右平移个单位而得到的，则函数图象的对称轴可以为（    ）

A．直线

B．直线

C．直线

D．直线

，且则的最小值为（  ）

A．

B．

C．

D．

函数的图象的一部分如图1所示，则此函数的解析
式为（  ）

A．

B．

C．

D．

若将函数的图象向右平移个单位，所得图象关于轴对称，则的最小正值是

A．

B．

C．

D．