高中数学多面角及多面角的性质选择题

下列函数中，最小正周期为且图象关于原点对称的函数是（）

A．	$y=\cos (2x+\frac{\pi }{2})$	B．	$y=\sin (2x+\frac{\pi }{2})$
C．	$y=\sin 2x+\cos 2x$	D．	$y=\sin x+\cos x$

已知点 $A$的坐标为 $(4\sqrt{3},1)$，将 $OA$绕坐标原点 $O$逆时针旋转 $\frac{\pi }{3}$至 $OB$，则点 $B$的纵坐标为（  ）

A．

$\frac{3\sqrt{3}}{2}$

B．

$\frac{5\sqrt{3}}{2}$

C．

$\frac{11}{2}$

D．

$\frac{13}{2}$

如图，某港口一天6时到18时的水深变化曲线近似满足函数 $y=\sin \left(\frac{\pi }{6}x+\phi \right)+k$ ，据此函数可知，这段时间水深（单位： $m$ ）的最大值为（）

A．

5

B．

6

C．

8

D．

10

要得到函数的图象，只需要将函数的图象（ ）

A．	向左平移 个单位
B．	向右平移 个单位
C．	向左平移 个单位
D．	向右平移 个单位

将函数 $f\left(x\right)=\sin 2x$的图像向右平移 $\phi \left(0<\phi <\frac{\pi }{2}\right)$个单位后得到函数 $g\left(x\right)$的图像,若对满足 $\left|f\left(x_1\right)-g\left(x_2\right)\right|=2$的 $x_1,x_2$,有 ${\left|x_1-x_2\right|}_{min}=\frac{\pi }{3}$,则 $\phi =$（）

A．

$\frac{5\pi }{12}$

B．

$\frac{\pi }{3}$

C．

$\frac{\pi }{4}$

D．

$\frac{\pi }{6}$

已知函数（均为正的常数）的最小正周期为，当时，函数取得最小值，则下列结论正确的是（）

A．
B．
C．
D．

函数的大致图象是（图中虚线是直线） （  ）

函数y=x+cosx的大致图象是（图中虚线是直线y="x" ）（   ）

若函数的图象在上恰有一个极大值和一个极小值，则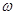 的取值范围是

A．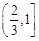

B．

C．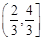

D．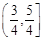

设函数的图象关于直线对称,它的最小正周期为，则（   ）

A．的图象过点

B．在上是减函数

C．的一个对称中心是

D．的一个对称中心是

函数 f (x)=" sin(2x" + 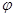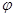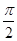）( || < )的图象向左平移 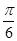个单位后关于原点对称， 则函数 f (x)在[0, 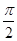]上的最小值为

A．－

B．－

C．

D．

函数的单调增区间是（ ）

A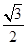．	B．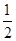
C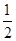．	D．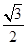

设函数f（x）=sin（2）+cos（2），且其图象关于直线x=0对称，则（     ）

A．y =f（x）的最小正周期为，且在（0，）上为增函数

B．y =f（x）的最小正周期为，且在（0，）上为增函数

C．y =f（x）的最小正周期为，且在（0，）上为减函数

D．y =f（x）的最小正周期为，且在（0，）上为减函数

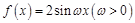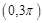若函数的图象在上恰有一个极大值和一个极小值，则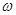的取值范围是

A．

B．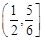

C．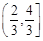

D．

已知函数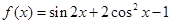，有下列四个结论：
①函数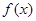在区间上是增函数；
②点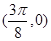是函数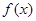图象的一个对称中心；
③函数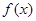的图象可以由函数的图象向左平移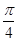得到；
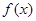④若，则的值域为．
则所有正确结论的序号是（   ）

A．①②③

B．①③

C．②④

D．①②