高中数学三角形的面积公式试题

安徽高考设△ABC的内角A，B，C所对边的长分别为a，b，c.若b＋c＝2a,3sin A＝5sin B，则角C＝(　　)

A．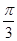

B．

C．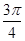

D．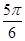

凸函数的性质定理:如果函数f(x)在区间D上是凸函数,则对于区间D内的任意x₁,x₂,…,x_n,有≤f,已知函数y="sin" x在区间(0,π)上是凸函数,则在△ABC中,sin A+sin B+sin C的最大值为　　　　.

某航模兴趣小组的同学，为了测定在湖面上航模航行的速度，采用如下办法：在岸边设置两个观察点A、B ，且 AB长为80米，当航模在C处时，测得∠ABC=105°和∠BAC=30°，经过20 秒后，航模直线航行到 D 处，测得 ∠BAD=90°和 ∠ABD=45°.请你根据以上条件求出航模的速度.（答案保留根号）

把函数的图象向左平移个单位长度后，所得到的图象关于y轴对称，则m的最小值是

A．

B．

C．

D．

定义在R上的函数既是偶函数又是周期函数，若的最小正周期是，且当时，，则的值为（      ）

A．	B．
C．	D．

已知函数，且函数的图象相邻两条对称轴之间的距离为.
（Ⅰ）求的值及的单调递增区间；
（Ⅱ）在中，分别是角的对边，若 求角

在中，角A，B，C所对的边分别为a，b，c，a=1,c=,
（1）求
（2）求的值
（3）求的值

为了得到函数的图象，可以将函数的图象（   ）

A．向右平移个单位长度	B．向右平移个单位长度
C．向左平移个单位长度	D．向左平移个单位长度

当0<x<时，函数f（x）=的最小值为 （   ）

A．2

B．2

C．4

D．4

在中，角A,B,C所对的边长分别为；若，；则（  ）

A．

B．

C．或

D．或

已知函数f（x）＝sin²x＋sinxcosx－（xÎR）．
（1）若，求f（x）的最大值；
（2）在△ABC中，若A＜B，f（A）＝f（B）＝，求  的值．

两点等分单位圆时，有相应正确关系为：三点等分单位圆时，有相应正确关系为：由此可以推知四点等分单位圆时的相应正确关系为__________

已知中，那么角=         

已知函数的最小正周期为，为了得到函数
的图象，只要将的图象  （      ）

A．向左平移个单位长度	B．向右平移个单位长度
C．向左平移个单位长度	D．向右平移个单位长度

右图是函数在区间上的图象。为了得到这个函数的图象，只要将的图象上所有的点（  ）

A．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变

B．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变

C．向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变

D．向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变