(8分)如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知 ,
, ,于A处测得水深
,于A处测得水深 ,于B处测得水深
,于B处测得水深 ,于C处测得水深
,于C处测得水深 ,求∠DEF的余弦值。
,求∠DEF的余弦值。
 |
一货轮航行到M处,测得灯塔S在货轮北偏东15º相距20海里处,随后货轮按北偏西30º的方向航行,半小时后,又测得灯塔在北偏东45º,求货轮的速度。
(本题满分12分) 中,
中, 分别是
分别是 的对边,且
的对边,且 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
(满分12分) 在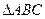 中,
中, 分别是角
分别是角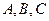 的对边,且
的对边,且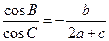 。
。
1)求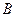 的大小;
的大小;
2)若 ,
,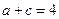 ,求
,求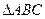 的面积。
的面积。
(本小题满分12分)
已知函数
 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点 处的切线的斜率是
处的切线的斜率是 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅲ)对任意给定的正实数 ,曲线
,曲线 上是否存在两点P、Q,使得
上是否存在两点P、Q,使得 是以O为直角顶点的直角三角形,且此三角形斜边中点在
是以O为直角顶点的直角三角形,且此三角形斜边中点在 轴上?说明理由。
轴上?说明理由。
(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c, 向量 p="(sinA,b+c), " q=(a-c,sinC-sinB),
满足|p +q |="|" p-q |.
(Ⅰ) 求角B的大小;
(Ⅱ)设m=(sin(C+ ),
), ),n="(2k,cos2A)" (k>1), m·n有最大值为3,求k的值.
),n="(2k,cos2A)" (k>1), m·n有最大值为3,求k的值.