已知 是
是 内的一点(不含边界),且
内的一点(不含边界),且
 ,若
,若 的面积分别为
的面积分别为 ,记
,记 ,则
,则 的最小值为
的最小值为
A. |
B. |
C. |
D. |
对大于 的自然数
的自然数 的三次幂可用奇数进行以下方式的“分裂”
的三次幂可用奇数进行以下方式的“分裂” 仿此,若
仿此,若 的“分裂”数中有一个是
的“分裂”数中有一个是 ,则
,则 的值为 .
的值为 .
已知 ,若函数
,若函数 在定义域内的一个区间
在定义域内的一个区间 上函数值的取值范围恰好是
上函数值的取值范围恰好是 ,则称区间
,则称区间 是函数
是函数 的一个减半压缩区间,若函数
的一个减半压缩区间,若函数 存在一个减半压缩区间
存在一个减半压缩区间 ,(
,( ),则实数m的取值范围是( )
),则实数m的取值范围是( )
A. |
B. |
C. |
D. |
对定义在区间D上的函数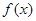 和
和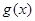 ,如果对任意
,如果对任意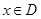 ,都有
,都有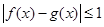 成立,那么称函数
成立,那么称函数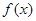 在区间D上可被
在区间D上可被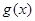 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
①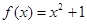 在区间
在区间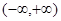 上可被
上可被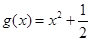 替代;
替代;
②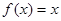 可被
可被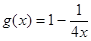 替代的一个“替代区间”为
替代的一个“替代区间”为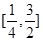 ;
;
③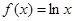 在区间
在区间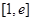 可被
可被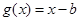 替代,则
替代,则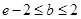 ;
;
④ ,则存在实数
,则存在实数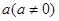 ,使得
,使得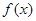 在区间
在区间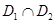 上被
上被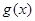 替代;
替代;
其中真命题的有
【原创】对定义在区间D上的函数 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
① 在区间
在区间 上可被
上可被 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③ 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
【原创】在实数集R中定义一种运算“*”,对任意a,b∈R,a*b为唯一确定的实数,且具有性质:
(1)对任意a∈R,a*0=a;
(2)对任意a,b∈R,a*b=ab+(a*0)+(b*0).
则函数f(x)=(ex)* 的最小值为是 .
的最小值为是 .
【原创】已知函数f(x)定义域为D,若∀a,b,c∈D,f(a),f(b),f(c)都是某一三角形的三边,则称f(x)为定义在D上的“保三角形函数”,以下说法正确的是 .
①f(x)=2(x∈R)不是R上的“保三角形函数”
②若定义在R上的函数f(x)的值域为[ ,2],则f(x)一定是R上的“保三角形函数”
,2],则f(x)一定是R上的“保三角形函数”
③f(x)= 是其定义域上的“保三角形函数”
是其定义域上的“保三角形函数”
④当t>1时,函数f(x)=ex+t一定是[0,1]上的“保三角形函数”
对于定义在 上的函数
上的函数 ,若存在距离为
,若存在距离为 的两条直线
的两条直线 和
和 ,使得对任意
,使得对任意 都有
都有 恒成立,则称函数
恒成立,则称函数 有一个宽度为
有一个宽度为 的通道.给出下列函数:
的通道.给出下列函数:
① ;②
;② ;③
;③ ;④
;④
其中在区间 上通道宽度可以为
上通道宽度可以为 的函数有 (写出所有正确的序号).
的函数有 (写出所有正确的序号).
定义符号函数  ,则下列结论中错误的是
,则下列结论中错误的是
A. |
B. |
C. |
D. |
若函数 满足
满足 (其中
(其中 不同时为0),则称函数
不同时为0),则称函数 为“准奇函数”,称点
为“准奇函数”,称点 为函数
为函数 的“中心点”。现有如下命题:
的“中心点”。现有如下命题:
①函数 是准奇函数;
是准奇函数;
②函数 是准奇函数;
是准奇函数;
③若准奇函数 在
在 上的“中心点”为
上的“中心点”为 ,则函数
,则函数 为
为 上的奇函数;
上的奇函数;
④已知函数 是准奇函数,则它的“中心点”为
是准奇函数,则它的“中心点”为 ;
;
其中正确的命题是 .(写出所有正确命题的序号)
函数 的定义域为D,若函数
的定义域为D,若函数 满足:(1)
满足:(1) 在D上为单调函数;(2)存在区间
在D上为单调函数;(2)存在区间 ,使得
,使得 在
在 上的值域为
上的值域为 ,则称函数
,则称函数 为“取半函数”。若
为“取半函数”。若
 ,且
,且 为“取半函数”,则
为“取半函数”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
若函数 满足对任意的
满足对任意的 ,都有
,都有 成立,则称函数
成立,则称函数 在区间
在区间 上是“被
上是“被 约束的”。若函数
约束的”。若函数 在区间
在区间 上是“被
上是“被 约束的”,则实数
约束的”,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
设函数 的定义域为
的定义域为 ,如果存在区间
,如果存在区间 ,使得
,使得 在区间
在区间 上的值域仍为
上的值域仍为 ,那么我们就把函数
,那么我们就把函数 叫做“保值函数”.若函数
叫做“保值函数”.若函数 为“保值函数”,则实数
为“保值函数”,则实数 的取值范围为
的取值范围为
A. |
B. |
C. |
D. |