【原创】对定义在区间D上的函数 和
和 ,如果对任意
,如果对任意 ,都有
,都有 成立,那么称函数
成立,那么称函数 在区间D上可被
在区间D上可被 替代,D称为“替代区间”.给出以下命题:
替代,D称为“替代区间”.给出以下命题:
① 在区间
在区间 上可被
上可被 替代;
替代;
② 可被
可被 替代的一个“替代区间”为
替代的一个“替代区间”为 ;
;
③ 在区间
在区间 可被
可被 替代,则
替代,则 ;
;
④ ,则存在实数
,则存在实数 ,使得
,使得 在区间
在区间 上被
上被 替代;
替代;
其中真命题的有
设函数 的定义域为
的定义域为 ,若函数
,若函数 满足条件:存在
满足条件:存在 ,使
,使 在
在 上的值域是
上的值域是 则称
则称 为“倍缩函数”,若函数
为“倍缩函数”,若函数 为“倍缩函数”,则的范围是( )
为“倍缩函数”,则的范围是( )
A. |
B. |
C. |
D. |
设函数 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使 对 一切实数x均成 立,则称
对 一切实数x均成 立,则称 为“倍约束函数”,现给出下列函数:
为“倍约束函数”,现给出下列函数:
① :
:
② :
:
③ ;
;
④
⑤ 是定义在实数集R上的奇函数,且对一切
是定义在实数集R上的奇函数,且对一切 均有
均有 ,
,
其中是“倍约束函数”的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设 与
与 是定义在同一区间
是定义在同一区间 上的两个函数,若对任意的
上的两个函数,若对任意的 ,都有
,都有 (
( ),则称
),则称 和
和 在
在 上是“
上是“ 度和谐函数”,
度和谐函数”, 称为“
称为“ 度密切区间”,设
度密切区间”,设 与
与 在
在 上是“
上是“ 度和谐函数”,则
度和谐函数”,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
【原创】如果函数 对定义域
对定义域 内的任意两个不相等的实数
内的任意两个不相等的实数 ,
, ,都有
,都有 ,则称函数
,则称函数 在定义域
在定义域 内为“
内为“ ”函数.以下函数为“
”函数.以下函数为“ ”函
”函
数的是( )
A. |
B. |
C. |
D. |
【原创】设函数 的定义域为
的定义域为 ,若存在常数
,若存在常数 ,使
,使 对一切实数
对一切实数 均
均
成立,则称 为“
为“ 函数”.现给出下列函数:
函数”.现给出下列函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则其中为“ 函数”的序号是( )
函数”的序号是( )
| A.①② | B.①④ | C.②③ | D.③④ |
【原创】设函数 在
在 上有意义,对给定正数
上有意义,对给定正数 ,定义函数
,定义函数 ,
,
则称函数 为
为 的“孪生函数”,若给定函数
的“孪生函数”,若给定函数 ,
, ,则
,则 ( )
( )
A. |
B. |
C. |
D. |
【原创】如果对定义在 上的函数
上的函数 ,对任意
,对任意 ,都有
,都有 ,
,
则称函数 为“
为“ 函数”.给出下列四个函数:
函数”.给出下列四个函数:
① ;②
;② ;③
;③ ;④
;④ .
.
则其中“ 函数”共有( )
函数”共有( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
【原创】已知点 ,点
,点 在曲线
在曲线 上,若线段
上,若线段 与曲线
与曲线 相交且交点恰为线段
相交且交点恰为线段 的中点,则称点
的中点,则称点 为曲线
为曲线 与曲线
与曲线 的一个“相关点”,记曲线
的一个“相关点”,记曲线 与曲线
与曲线 的“相关点”的个数为
的“相关点”的个数为 ,则 ( )
,则 ( )
A. |
B. |
C. |
D. |
函数 的定义域为A,若
的定义域为A,若 且
且
 时总有
时总有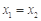 ,则称
,则称 为单函数.例如,函数
为单函数.例如,函数 =2x+1(
=2x+1( )是单函数.下列命题:
)是单函数.下列命题:
①函数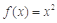 (x
(x R)是单函数;
R)是单函数;
②指数函数 (x
(x R)是单函数;
R)是单函数;
③若 为单函数,
为单函数, 且
且 ,则
,则 ;
;
④在定义域上具有单调性的函数一定是单函数.
其中的真命题是_________.(写出所有真命题的编号)
定义在R上的函数 ,若对任意
,若对任意 ,都有
,都有 ,则称f(x)为“H函数”,给出下列函数:
,则称f(x)为“H函数”,给出下列函数:
① ;
;
② ;
;
③ ;
;
④
其中是“H函数”的个数为( )
| A.4 | B.3 | C.2 | D.1 |
对于三次函数 ,给出定义:设
,给出定义:设 是函数y=f(x)的导数,
是函数y=f(x)的导数, 是
是 的导数,若方程
的导数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
为函数y=f(x)的“拐点”.某同学经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.
设函数 ,则
,则 =( )
=( )
| A.2014 | B.2013 | C. |
D.1007 |
 为实数,
为实数, 表示不超过
表示不超过 的最大整数,则函数
的最大整数,则函数 在
在 上为
上为
| A.增函数 | B.周期函数 | C.奇函数 | D.偶函数 |