高中数学不定方程和方程组填空题

实系数一元二次方程有两个根，一个根在区间（0,1）内，另一个根在区间（1,2）内，则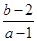的取值范围________．

已知，（其中为自然对数的底数），方程有四个实数根，则实数的取值范围为             ．

若函数有两个零点，则实数的取值范围是______________．

已知函数，则函数的图象与轴有        个交点．

若直线y＝x＋b与曲线y＝有公共点，则b的取值范围是________．

已知函数与的图像有3个不同的公共点（其中e为自然对数的底数），则实数a的取值范围是_______________．

函数，若在区间上有零点，则实数的取值范围为                            ．

下列几个命题：
①函数是偶函数，但不是奇函数；
②方程的有一个正实根，一个负实根，则；
③是定义在R上的奇函数，当x＜0时，＝，则x≥ 0时，＝

④函数的值域是．
其中正确的有          ．

A．②④

B．①③④

C．①②④

D．①②③

己知函数f（x）=X²-1，则函数f（x-1)的零点是        ．

已知偶函数满足，且当时，，若在区间内，函数有4个零点，则实数的取值范围是           ．

已知函数，给出下列四个命题：
①存在实数，使得函数恰有2个不同的零点；
②存在实数，使得函数恰有4个不同的零点；
③存在实数，使得函数恰有5个不同的零点；
④存在实数，使得函数恰有8个不同的零点．
其中真命题的序号是（把你认为正确的序号全写上）．

设，若，且，则的取值范围为     ．

已知函数若存在实数使得则的取值范围为     ．

已知函数．给出下列命题：
①是偶函数；
②当＝时，的图象关于直线对称；
③若≤0，则在区间上是增函数；
④有最小值；
⑤若方程恰有3个不相等的实数根，则．
其中正确命题的序号是         ．

已知函数，若且，则的取值范围是            ．