若函数 满足
满足 且
且 时,
时, ,函数
,函数 分别在两相邻对称轴
分别在两相邻对称轴 与
与 处取得最值1与
处取得最值1与 ,则函数
,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.1006 | B.1007 | C.1008 | D.1010 |
设定义在 的单调函数
的单调函数 ,对任意的
,对任意的 都有
都有 .若
.若 是方程
是方程 的一个解,且
的一个解,且 ,则实数
,则实数 ( )
( )
| A.4 | B.3 | C.2 | D.1 |
设函数 是定义在R上的奇函数,当
是定义在R上的奇函数,当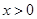 时,
时,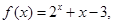 则
则 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
【原创】函数 的图象向右平移一个单位后得到的函数图象与函数
的图象向右平移一个单位后得到的函数图象与函数 的图象所有交点的橫坐标之和等于( )
的图象所有交点的橫坐标之和等于( )
| A.2 | B.4 | C.6 | D.8 |
设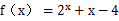 ,则函数
,则函数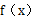 的零点位于区间( )
的零点位于区间( )
| A.(2,3) | B.(1,2) | C.(0,1) | D.(-1,0) |
用反证法证明命题:“设 为实数,则函数
为实数,则函数 至多有两个零点”时,要做的假设是
至多有两个零点”时,要做的假设是
A.函数 至少有三个零点 至少有三个零点 |
B.函数 只有两个零点 只有两个零点 |
C.函数 至少有两个零点 至少有两个零点 |
D.函数 没有零点 没有零点 |
函数 ,则下列命题中正确命题的个数是( ).
,则下列命题中正确命题的个数是( ).
①函数 有
有 个零点;
个零点;
②若 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 ;
;
③函数 的极大值中一定存在最小值;
的极大值中一定存在最小值;
④
 ,对一切
,对一切 恒成立.
恒成立.
A. |
B. |
C. |
D. |
设 ,若函数
,若函数 在区间
在区间 上有三个零点,则实数
上有三个零点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 ,若
,若 的图像与
的图像与 轴有
轴有 个不同的交点,则实数
个不同的交点,则实数 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |