期中备考总动员高三理数学模拟卷【浙江】8
若函数 满足
满足 且
且 时,
时, ,函数
,函数 分别在两相邻对称轴
分别在两相邻对称轴 与
与 处取得最值1与
处取得最值1与 ,则函数
,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.1006 | B.1007 | C.1008 | D.1010 |
要得到一个奇函数,只需将 的图象( )
的图象( )
A.向右平移 个单位 个单位 |
B.向右平移 个单位 个单位 |
C.向左平移 个单位 个单位 |
D.向左平移 个单位 个单位 |
在三棱柱 种侧棱垂直于底面,
种侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱 的体积为3,则三棱柱
的体积为3,则三棱柱 的外接球的表面积为( )
的外接球的表面积为( )
A. |
B. |
C. |
D. |
已知点 ,若
,若 为双曲线
为双曲线 的右焦点,
的右焦点, 是该双曲线上且在第一象限的动点,则
是该双曲线上且在第一象限的动点,则 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
若定义在 上的函数
上的函数 满足,且当
满足,且当 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点的个数为( )
内的零点的个数为( )
| A.6 | B.7 | C.8 | D.9 |
已知实数 ,
, 满足
满足 ,若目标函数
,若目标函数 的最大值与最小值的差为
的最大值与最小值的差为 ,则实数
,则实数 的值为 ;不等十足表示的平面区域的面积为 .
的值为 ;不等十足表示的平面区域的面积为 .
定义“兄函数”运算 ,设函数
,设函数 ,若函数
,若函数 恰有一个零点,则实数
恰有一个零点,则实数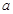 的取值范围是 ;若函数
的取值范围是 ;若函数 恰有三个零点,则实数
恰有三个零点,则实数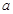 的取值范围是 .
的取值范围是 .
定义: 表示
表示 两个数中的最大值,
两个数中的最大值,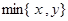 表示
表示 两个数中的最小值.给出下列4个命题:①
两个数中的最小值.给出下列4个命题:①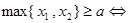
 且
且 ;②
;②
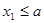 且
且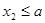 ;③设函数
;③设函数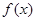 和
和 的公共定义域为
的公共定义域为 ,若
,若 ,
,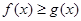 恒成立,则
恒成立,则 ;④若函数
;④若函数 的图象关于直线
的图象关于直线 对称,则
对称,则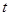 的值为
的值为 .其中真命题是 .(写出所有真命题的序号)
.其中真命题是 .(写出所有真命题的序号)
(本小题满分15分)已知 ,且
,且 ,设
,设 ,
, 的图象相邻两对称轴之间的距离等于
的图象相邻两对称轴之间的距离等于 .
.
(Ⅰ)求函数 的解析式;
的解析式;
(Ⅱ)在△ABC中, 分别为角
分别为角 的对边,
的对边, ,
, ,求
,求 面积的最大值.
面积的最大值.
(本小题满分15分)设数列 为等差数列,且
为等差数列,且 ;数列
;数列 的前
的前 项和为
项和为 .
.
(Ⅰ)求数列 ,
, 的通项公式;
的通项公式;
(Ⅱ)若 为数列
为数列 的前
的前 项和,求
项和,求 .
.
(本小题满分15分)如图,在直三棱柱 中,平面
中,平面
 侧面
侧面 且
且 .
.

(Ⅰ)求证: ;
;
(Ⅱ)若直线AC与平面 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小.
的大小.
(本小题满分15分)已知椭圆 的离心率为
的离心率为 ,其左焦点
,其左焦点 到点
到点 的距离为
的距离为 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过右焦点 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点 、
、 ,则
,则 内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
内切圆的圆面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.
 ,且
,且 的集合
的集合 的个数是( )
的个数是( ) 满足
满足 并且
并且 ,则数列
,则数列



 上,且与直线
上,且与直线 相切的面积最小的圆的方程为( )
相切的面积最小的圆的方程为( )



 的内角
的内角 ,
, ,
, 所对的边
所对的边 ,
, ,
, 向量
向量 且
且 ,则
,则 ;若
;若 ,则
,则
 与直线
与直线 交于
交于 ,抛物线
,抛物线 上一点
上一点 ,若
,若 面积的最小值为
面积的最小值为 ,则点
,则点 所在的平面内,点
所在的平面内,点 满足
满足 ,
, ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
 , 则 .
, 则 . .
. ,
, 对一切
对一切 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; ,且
,且 、
、 是曲线
是曲线 上任意两点,若对任意
上任意两点,若对任意 ,直线
,直线 的斜率恒大于常数
的斜率恒大于常数 ,求实数
,求实数 粤公网安备 44130202000953号
粤公网安备 44130202000953号