一个口袋中装有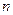 个红球(
个红球(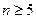 且
且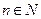 )和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
)和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试用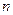 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率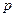 ;
;
(Ⅱ)若 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(Ⅲ)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为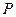 .当
.当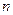 取多少时,
取多少时,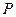 最大?
最大?
(新华网)反兴奋剂的大敌、服药者的宠儿——HGH(人体生长激素),有望在2008年8月的北京奥运会上首次“伏法”。据悉,国际体育界研究近10年仍不见显著成效的HGH检测,日前已取得新的进展,新生产的检测设备有希望在北京奥运会上使用.若组委会计划对参加某项比赛的12名运动员的血样进行突击检查,采用如下化验方法:将所有待检运动员分成若干小组,每组m个人,再把每个人的血样分成两份,化验时将每个小组内的m个人的血样各一份混合在一起进行化验,若结果中不含HGH成分,那么该组的m个人只需化验这一次就算检验合格;如果结果中含有HGH成分,那么需要对该组进行再次检验,即需要把这m个人的另一份血样逐个进行化验,才能最终确定是否检验合格,这时,对这m个人一共需要进行m+1次化验.假定对所有人来说,化验结果中含有HGH成分的概率均为 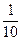 .当m=3时,求:
.当m=3时,求:
(1)一个小组只需经过一次检验就合格的概率;
(2)至少有两个小组只需经过一次检验就合格的概率(精确到0.01.参考数据:0.2713≈0.020,0.2714≈0.005,0.7292≈0.500)
某人对一目标进行射击,每次命中率都是0.25,若使至少命中1次的概率不小于0.75,至少应射击几次?
甲投篮命中率为O.8,乙投篮命中率为0.7,每人投3次,两人恰好都命中2次的概率是多少?
设一次试验成功的概率为p,现进行16次独立重复试验.当p=__________时,成功次数的标准差最大,其最大值为__________.
某家具制造商购买的每10块板中平均有1块是不能用于做家具的,一组5块这样的板中有3块或4块可用的概率约为( )
| A.0.40 | B.0.3 | C.0.07 | D.0.2 |
某气象站天气预报的准确率为 ,计算(结果保留到小数点后面第2位)
,计算(结果保留到小数点后面第2位)
(1)5次预报中恰有2次准确的概率;
(2)5次预报中至少有2次准确的概率;
(3)5次预报中恰有2次准确,且其中第 次预报准确的概率
次预报准确的概率
一份航空意外伤害保险保险费为20元,保险金额为45万元.如果某城市的一家保险公司一年能销售这种保单10万份,所需成本为5万元,而需要赔付的概率为 .那么请问1年内赔付人数为多少时,这家保险公司会亏本?
.那么请问1年内赔付人数为多少时,这家保险公司会亏本?
一台X型号自动机床在一小时内不需要工人照看的概率为0.8,有四台这种型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 ( )
| A.0.1536 | B.0.1808 | C.0.5632 | D.0.9728 |
10.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)等于
A.C ( ( )10·( )10·( )2 )2 |
B.C ( ( )9( )9( )2· )2· |
C.C ( ( )9·( )9·( )2 )2 |
D.C ( ( )9·( )9·( )2 )2 |