如图,在三棱锥P—ABC中,G、H分别为PB、PC的中点,且△ABC为等腰直角三角形,∠B=90°.
⑴求证:GH∥平面ABC;
⑵求异面直线GH与AB所成的角.
在长方体 中,
中, ,过
,过 ,
, ,
, 三点的平面截去长方体的一个角后,得到如图所示的几何体
三点的平面截去长方体的一个角后,得到如图所示的几何体 ,这个几何体的体积为
,这个几何体的体积为 .
.
(1)证明:直线 ∥平面
∥平面 ;
;
(2)求棱 的长;
的长;
(3)在线段 上是否存在点
上是否存在点 ,使直线
,使直线 与
与 垂直,如果存在,求线段
垂直,如果存在,求线段 的长,如果不存在,请说明理由.
的长,如果不存在,请说明理由.
如图,在五面体 中,已知
中,已知 平面
平面 ,
, ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
如图,四边形ABCD为正方形,PD⊥平面ABCD, ,AF⊥PC于点F,FE∥CD交PD于点E.
,AF⊥PC于点F,FE∥CD交PD于点E.
(1)证明:CF⊥平面ADF;
(2)若 ,证明
,证明 平面
平面
如图已知:菱形 所在平面与直角梯形ABCD所在平面互相垂直,
所在平面与直角梯形ABCD所在平面互相垂直, ,
, 点
点 分别是线段
分别是线段 的中点.
的中点. 
(1)求证:平面
 平面
平面 ;
;
(2)试问在线段 上是否存在点
上是否存在点 ,使得
,使得
 平面
平面 ,若存在,求
,若存在,求 的长并证明;若不存在,说明理由.
的长并证明;若不存在,说明理由.
如图,四棱锥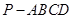 中,侧面
中,侧面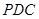 是边长为2的正三角形,底面
是边长为2的正三角形,底面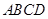 是菱形,
是菱形,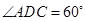 ,点
,点 在底面
在底面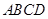 上的射影为
上的射影为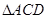 的重心,点
的重心,点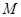 为线段
为线段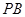 上的点.
上的点.
(1)当点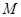 为
为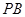 的中点时,求证:
的中点时,求证: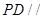 平面
平面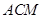 ;
;
(2)当平面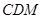 与平面
与平面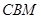 所成锐二面角的余弦值为
所成锐二面角的余弦值为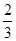 时,求
时,求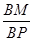 的值.
的值.
已知E是矩形ABCD(如图1)边CD上的一点,现沿AE将△DAE折起至△D1AE(如图2),并且平面D1AE⊥平面ABCE,图3为四棱锥D1—ABCE的主视图与左视图.

(1)求证:直线BE⊥平面D1AE;
(2)求点A到平面D1BC的距离.
如图,在多面体 中,四边形
中,四边形 是正方形,
是正方形, .
. .
.
(Ⅰ) 求证: ;
;
(Ⅱ)求二面角 的余弦值的大小.
的余弦值的大小.
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.
(1)若AB BC,CP
BC,CP PB,求证:CP
PB,求证:CP PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.