利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )

| A.46 | B.48 | C.50 | D.52 |
为了解一大片经济林生长情况,随机测量其中的60株的底部周长(单位:Cm),将周长整理后画出的频率分布表和频率分布直方图如下:观察图形,回答下列问题:
| 组距 |
频数 |
频率 |
|
 [ [ |
6 |
0.1 |
|
 |
|
0.15 |
|
 |
9 |
|
|
 |
18 |
|
|
 |
|
0.25 |
|
 |
3 |
0.05 |
|
| 合计 |
|
|

(1)补充上面的频率分布表和频率分布直方图.
(2)79.5~89.5 这一组的频数、频率分别是多少?
(3)估计这次环保知识竞赛的及格率(60cm及以上为合格
在样本频率分布直方图中,共有9个小长方形,若中间一个小长方形的面积等于其他8个长方形面积和的 ,且样本容量为140,则中间一组的频数为( )
,且样本容量为140,则中间一组的频数为( )
A. |
B. |
C. |
D. |
在抽查产品的尺寸过程中,将其尺寸分成若干组. 是其中的一组,抽查出的个体在该组上的频率为m,该组上的直方图的高为h,则
是其中的一组,抽查出的个体在该组上的频率为m,该组上的直方图的高为h,则 =
=
| A.hm | B. |
C. |
D.h+m |
甲乙两个数学兴趣小组各有5名同学,在一次数学测试中,成绩统计用茎叶图表示,如图所示,若甲、乙小组的平均成绩分别是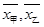 ,则下列结论正确的是( )
,则下列结论正确的是( )
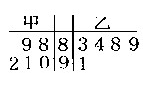
A. ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
B. ,乙比甲成绩稳定 ,乙比甲成绩稳定 |
C.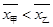 ,甲比乙成绩稳定 ,甲比乙成绩稳定 |
D.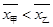 ,乙比甲成绩稳定 ,乙比甲成绩稳定 |
一个社会调查机构就某地居民的月收入调查了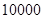 人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这
人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这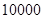 人中再用分层抽样方法抽出
人中再用分层抽样方法抽出 人作进一步调查,则在
人作进一步调查,则在 (元)月收入段应抽出 人.
(元)月收入段应抽出 人.

从甲乙两个城市分别随机抽取10台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为 ,
, ,中位数分别为
,中位数分别为 ,
, ,则( )
,则( )

A. |
B. |
C. |
D. |
某学校组织学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为
 若低于60分的人数是15人,则该班的学生人数是 ( )
若低于60分的人数是15人,则该班的学生人数是 ( )

A. |
B. |
C. |
D. |
为了了解学生的视力情况,随机抽查了一批学生的视力,将抽查结果绘制成频率分布直方图(如图所示).若在[5.0,5.4]内的学生人数是2,则根据图中数据可得被样本数据在[3.8,4.2)内的人数是 .

一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别为( )
| A.57.2 3.6 | B.57.2 56.4 | C.62.8 63.6 | D.62.8 3.6 |
如图是 年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )

| A.84,84 | B.84,85 | C.85,84 | D.85,85 |
某苗圃基地为了了解基地内甲、乙两块地种植的同一种树苗的长势情况,从两块地各随机抽取了10株树苗,用如图所示的茎叶图表示上述两组数据.对两块地抽取树苗的高度的平均数  甲,
甲, 乙和中位数
乙和中位数 甲,
甲, 乙进行比较,下面结论正确的是
乙进行比较,下面结论正确的是

A. 甲> 甲> 乙, 乙, 甲> 甲> 乙 乙 |
B. 甲< 甲< 乙, 乙, 甲< 甲< 乙 乙 |
C. 甲< 甲< 乙, 乙, 甲> 甲> 乙 乙 |
D. 甲> 甲> 乙, 乙, 甲< 甲< 乙 乙 |
某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则 的值为( )
的值为( )

| A.9 | B.10 | C.11 | D.13 |