在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
下列命题中,真命题是 (将真命题前面的编号填写在横线上).
①已知平面 、
、 和直线
和直线 、
、 ,若
,若 ,
, 且
且 ,则
,则 .
.
②已知平面 、
、 和两异面直线
和两异面直线 、
、 ,若
,若 ,
, 且
且 ,
, ,则
,则 .
.
③已知平面 、
、 、
、 和直线
和直线 ,若
,若 ,
, 且
且 ,则
,则 .
.
④已知平面 、
、 和直线
和直线 ,若
,若 且
且 ,则
,则 或
或 .
.
在直三棱柱 中,若
中,若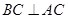 ,
, ,
, ,
, 为
为 中点,点
中点,点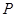
为 中点,
中点, 在线段
在线段 上,且
上,且 ,则
,则 的长度为________ .
的长度为________ .
 表示直线,
表示直线, 表示平面,给出下列四个命题:
表示平面,给出下列四个命题:
①若  则
则  ;
;
②若 ,则
,则  ;
;
③若 ,则
,则  ;
;
④若  ,则
,则  .
.
其中正确命题的个数有 ________个.
若 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线 ,则在平面
,则在平面 内,一定不存在与直线
内,一定不存在与直线 平行的直线.
平行的直线.
②若直线 ,则在平面
,则在平面 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线 垂直.
垂直.
③若直线 ,则在平面
,则在平面 内,不一定存在与直线
内,不一定存在与直线 垂直的直线.
垂直的直线.
④若直线 ,则在平面
,则在平面 内,一定存在与直线
内,一定存在与直线 垂直的直线.
垂直的直线.
若 是互不重合的直线,
是互不重合的直线,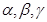 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题:
①若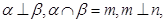 则
则 或
或 ;
;
②若 则
则 ;
;
③若 不垂直于
不垂直于 ,则
,则 不可能垂直于
不可能垂直于 内的无数条直线;
内的无数条直线;
④若 且
且 则
则
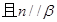 ;
;
⑤若 且
且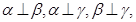 则
则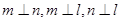 .
.
其中正确命题的序号是 .
若 是互不重合的直线,
是互不重合的直线, 是互不重合的平面,给出下列命题:
是互不重合的平面,给出下列命题:
①若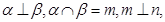 则
则 或
或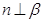 ;
;
②若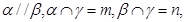 则
则 ;
;
③若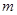 不垂直于
不垂直于 ,则
,则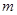 不可能垂直于
不可能垂直于 内的无数条直线;
内的无数条直线;
④若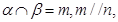 且
且 则
则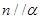
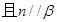 ;
;
⑤若 且
且 则
则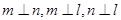 .
.
其中正确命题的序号是 .
如图,设P是60 的二面角
的二面角  内一点,PA
内一点,PA  平面
平面  ,PB
,PB  平面
平面  ,A、B为垂足若PA=4.PB=2,则AB的长为_______.
,A、B为垂足若PA=4.PB=2,则AB的长为_______.
下列说法中:
①两条直线都和同一个平面平行,则这两条直线平行;
②在平行投影下,与投影面平行的平面图形留下的影子,与这个平面图形的形状和大小完全相同;
③一个圆绕其任意一条直径旋转180°所形成的旋转体叫做球;
④a∥b,b⊂α⇒a∥α;
⑤已知三条两两异面的直线,则存在无穷多条直线与它们都相交.
则正确的序号是 .
给出下列结论:
①函数 在区间
在区间 上有且只有一个零点;
上有且只有一个零点;
②已知l是直线, 是两个不同的平面.若
是两个不同的平面.若 ;
;
③已知 表示两条不同直线,
表示两条不同直线, 表示平面.若
表示平面.若 ;
;
④在 中,已知
中,已知 ,在求边c的长时有两解.
,在求边c的长时有两解.
其中所有正确结论的序号是:
已知PA⊥正方形ABCD所在的平面,垂足为A,连结PB,PC,PD,则平面PAB,平面PAD,平面PCD,平面PBC,平面ABCD中互相垂直的平面有 对 
在四棱锥P—ABCD中,侧面PAD、侧面PCD与底成ABCD都垂直,底面是边长为3的正方形,PD=4,则四棱锥P—ABCD的全面积为 .
在正方体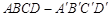 中,过对角线
中,过对角线 的一个平面交棱
的一个平面交棱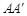 于E,交棱
于E,交棱 于F,则:①四边形
于F,则:①四边形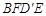 一定是平行四边形;②四边形
一定是平行四边形;②四边形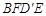 有可能是正方形;③四边形
有可能是正方形;③四边形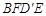 有可能是菱形;④四边形
有可能是菱形;④四边形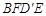 有可能垂直于平面
有可能垂直于平面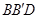 .
.
其中所有正确结论的序号是 .