点P为ΔABC所在平面外一点,PO⊥平面ABC,垂足为O,若PA=PB=PC,则点O是ΔABC的( )
A 内心 B 外心 C 重心 D 垂心
给定下列四个命题:
①若一个平面内的两条直线与另外一个平面都平行,那么这两个平面相互平行;
②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;
③垂直于同一直线的两条直线相互平行;
④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直。
其中,为真命题的是( )
| A.①和② | B.②和③ | C.③和④ | D.②和④ |
如图,正方形AB1 B2 B3中,C,D分别 是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成
是B1 B2 和B2 B3的中点,现沿AC,AD及CD把这个正方形折成 一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体
一个四面体,使B1 ,B2 ,B3三点重合,重合后的点记为B,则四面体
A—BCD中,互相垂直的面共有( )
| A.4对 | B.3对 | C.2对 | D.1 对 对 |

一个三棱锥,如果它的底面是直角三角形,那么它的三个侧面( )
| A.必定都不是直角三角形 | B.至多有一个直角三角形 |
| C.至多有两个直角三角形 | D.可能都是直角三角形 |
如图,设平面 垂足分别是B、D,如果增加一个条件,就能推出
垂足分别是B、D,如果增加一个条件,就能推出 EF,这个条件不可能是下面四个选项中的( )
EF,这个条件不可能是下面四个选项中的( )
A. 
B. 
C. AC与BD在b内的射影在同一条直线上
D.  与a、b所成的角相等
与a、b所成的角相等
 ,
, 为两个互相垂直的平面,a、b为一对异面直线,下列条件:
为两个互相垂直的平面,a、b为一对异面直线,下列条件:
①a// 、b
、b ;②a⊥
;②a⊥ 、b
、b ;③a⊥
;③a⊥ 、b
、b ;④a//
;④a// 、b
、b 且a与
且a与 的距离等于b与
的距离等于b与 的距离,其中是a⊥b的充分条件的有 ( )
的距离,其中是a⊥b的充分条件的有 ( ) 
| A.①④ | B.① | C.③ | D.②③ |
四面体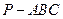 中,若
中,若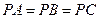 ,则点
,则点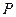 在平面
在平面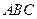 内的射影点
内的射影点 是
是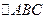 的 ( )
的 ( )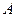 、外心;
、外心; 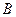 、内心;
、内心; 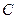 、垂心;
、垂心; 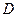 、重心。
、重心。
已知集合A={直线},B={平面}, ,若
,若 ,给定下列命题:
,给定下列命题:
① ;②
;② ;③
;③ ;④
;④ .
.
其中一定正确的是( )
| A.①② | B.②③ | C.③④ | D.② |
在正四面体P—ABC中,D、E、F分别是AB、BC、CA的中点,下列四个结论中不成立的是( )
| A.BC//平面PDF | B.DF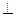 平面PAE 平面PAE |
C.平面PDF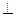 平面ABC 平面ABC |
D.平面PAE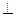 平面ABC 平面ABC |
已知两个平面垂直,下列命题 一个平面内已知直线必垂直于另一个平面内的任意一条直线.
一个平面内已知直线必垂直于另一个平面内的任意一条直线. 一个平面内的已知直线必垂直于另一个平面的无数条直线.
一个平面内的已知直线必垂直于另一个平面的无数条直线. 一个平面内的任一条直线必垂直于另一个平面.
一个平面内的任一条直线必垂直于另一个平面. 过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
过一个平面内任意一点作交线的垂线,则此垂线必垂直于另一个平面.
其中正确的个数是( )
| A.3 | B.2 | C.1 | D.0 |