如图,已知六棱锥P﹣ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB则下列结论正确的是( )

| A.PB⊥AD |
| B.平面PAB⊥平面PBC |
| C.直线BC∥平面PAE |
| D.直线PD与平面ABC所成的角为45° |
如图所示,在直三棱柱ABC-A1B1C1中, BC="AC" ,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1 ,③平面AMC1⊥平面CBA1 ,其中正确结论的个数为 ( )

| A.0 | B.1 | C.2 | D.3 |
如图所示,在直三棱柱ABC-A1B1C1中,BC=AC,AC1⊥A1B,M,N分别是A1B1,AB的中点,给出下列结论:①C1M⊥平面A1ABB1,②A1B⊥NB1 ,③平面AMC1//平面CNB1, 其中正确结论的个数为 ( )

| A.0 | B.1 | C.2 | D.3 |
在四棱柱 中,
中, 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 的长为
的长为 ,
, 为侧棱
为侧棱 上的动点(包括端点),则( )
上的动点(包括端点),则( )
A.对任意的 , , ,存在点 ,存在点 ,使得 ,使得 |
B.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
C.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
D.当且仅当 时,存在点 时,存在点 ,使得 ,使得 |
如下图,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD= .在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )

| A.面ABD⊥面BCD | B.面ABD⊥面ACD |
| C.面ABC⊥面ACD | D.面ABC⊥面BCD |
如图,等边三角形 的中线
的中线 与中位线
与中位线 相交于
相交于 ,已知
,已知 是△
是△ 绕
绕 旋转过程中的一个图形,下列命题中,错误的是( )
旋转过程中的一个图形,下列命题中,错误的是( )
A.动点 在平面 在平面 上的射影在线段 上的射影在线段 上 上 |
B.恒有平面 ⊥平面 ⊥平面 |
C.三棱锥 的体积有最大值 的体积有最大值 |
D.异面直线 与 与 不可能垂直 不可能垂直 |

如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=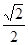 ,则下列结论中错误的个数是( )
,则下列结论中错误的个数是( )
(1) AC⊥BE.
(2) 若P为AA1上的一点,则P到平面BEF的距离为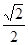 .
.
(3) 三棱锥A-B EF的体积为定值.
EF的体积为定值.
(4) 在空间与DD1,AC,B1C1都相交的直线有无数条.
(5) 过CC1的中点与直线AC1所成角为40并且与平面BEF所成角为50的直线有2条.
| A.0 | B.1 | C.2 | D.3 |
下面四个命题:
①“直线a∥直线b”的充要条件是“a平行于b所在的平面”;
②“直线 ⊥平面
⊥平面 内所有直线”的充要条件是“
内所有直线”的充要条件是“ ⊥平面
⊥平面 ”;
”;
③“直线a、b为异面直线”的充分不必要条件是“直线a、b不相交”;
④“平面 ∥平面
∥平面 ”的必要不充分条件是“
”的必要不充分条件是“ 内存在不共线三点到
内存在不共线三点到 的距离相等”;
的距离相等”;
其中正确命题的序号是
| A.①② | B.②③ | C.③④ | D.②④ |
已知 是直线,
是直线,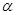 是平面,
是平面, 、
、
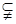
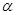 ,则“
,则“ 平面
平面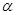 ”是“
”是“ 且
且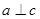 ”的 ………………………………………………………………………… ( )
”的 ………………………………………………………………………… ( )
| A.充要条件. | B.充分非必要条件. | C.必要非充分条件. | D.非充分非必要条件 |