期中备考总动员高三文数学模拟卷【浙江】5
如下图,在平行四边形ABCD中,AD=2AB=2,∠BAC=90°.将△ACD沿AC折起,使得BD= .在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )
.在三棱锥D-ABC的四个面中,下列关于垂直关系的叙述错误的是( )

| A.面ABD⊥面BCD | B.面ABD⊥面ACD |
| C.面ABC⊥面ACD | D.面ABC⊥面BCD |
设不等式组 表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
表示的平面区域为D.若圆C:(x+1)2+(y+1)2=r2(r>0)不经过区域D上的点,则r的取值范围是( )
A.[2 ,2
,2 ] B.[2
] B.[2 ,3
,3 ]
]
C.[3 ,2
,2 ] D.(0,2
] D.(0,2 )∪(2
)∪(2 ,+∞)
,+∞)
将函数 的图象向右平移
的图象向右平移 个单位后得到函数
个单位后得到函数 ,则
,则 具有性质( )
具有性质( )
A.最大值为 ,图象关于直线 ,图象关于直线 对称 对称 |
B.在 上单调递增,为奇函数 上单调递增,为奇函数 |
C.在 上单调递增,为偶函数 上单调递增,为偶函数 |
D.周期为 ,图象关于点 ,图象关于点 对称 对称 |
已知点 ,
, ,
, 是直线
是直线 上任意一点,以
上任意一点,以 ,
, 为焦点的椭圆过
为焦点的椭圆过 ,记椭圆离心率
,记椭圆离心率 关于
关于 的函数为
的函数为 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A. 与 与 一 一对应 一 一对应 |
B.函数 无最小值,有最大值 无最小值,有最大值 |
C.函数 是增函数 是增函数 |
D.函数 有最小值,无最大值 有最小值,无最大值 |
(原创)一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的体积为 ;该几何体的外接球的表面积为 .

(原创)设函数 图象的一条对称轴是直线
图象的一条对称轴是直线 ,则
,则 __________;
__________; 图象的对称中心坐标是_________.
图象的对称中心坐标是_________.
设P,Q为一个正方体表面上的两点,已知此正方体绕着直线PQ旋转 (
( )角后能与自身重合,那么符合条件的直线PQ有_____条.
)角后能与自身重合,那么符合条件的直线PQ有_____条.
对于函数 ,有下列4个命题:
,有下列4个命题:
①任取 ,都有
,都有 恒成立;
恒成立;
②
 ,对于一切
,对于一切 恒成立;
恒成立;
③函数 有3个零点;
有3个零点;
④对任意 ,不等式
,不等式 恒成立.
恒成立.
则其中所有真命题的序号是 .
(原创)已知{ }是公比为q的等比数列,且
}是公比为q的等比数列,且 成等差数列.
成等差数列.
(1)求q的值;
(2)设数列 的前
的前 项和为
项和为 ,试判断
,试判断 是否成等差数列?说明理由.
是否成等差数列?说明理由.
(本小题满分15分)在△ABC中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,设S为△ABC的面积,满足
,设S为△ABC的面积,满足 .
.
(Ⅰ)求角C的大小;
(Ⅱ)若 ,且
,且 ,求
,求 的值.
的值.
如图,四边形 为矩形,
为矩形, 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
.
(1)求三棱锥 的体积;
的体积;
(2)设 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.
在平面直角坐标系 中,点
中,点 为动点,
为动点, 、
、 分别为椭圆
分别为椭圆 的左、右焦点.已知
的左、右焦点.已知 为等腰三角形.
为等腰三角形.
(1)求椭圆的离心率 ;
;
(2)设直线 与椭圆相交于
与椭圆相交于 、
、 两点,
两点, 是直线
是直线 上的点,满足
上的点,满足 ,求点
,求点 的轨迹方程.
的轨迹方程.
 ,集合
,集合 则集合
则集合 =( )
=( )
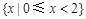

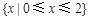
 中有两项
中有两项 满足
满足 ,
, ,则该数列前m+k项之和是 ( )
,则该数列前m+k项之和是 ( )




 为互不相等的正数,
为互不相等的正数, ,则下列关系中可能成立的是( )
,则下列关系中可能成立的是( )



 满足
满足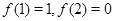 对任意
对任意
 ,当
,当 时恒有
时恒有 ,则
,则 =( )
=( ) 的前n项和为
的前n项和为 ,若
,若 且
且 是公比为2的等比数列,则
是公比为2的等比数列,则 ;
; .
. 表示的平面区域
表示的平面区域 的面积为
的面积为 ,则
,则 ;
; ,则
,则 的最小值为 .
的最小值为 . ,直线
,直线 为直线
为直线 上一点,若圆
上一点,若圆 上存在两点
上存在两点 ,使得
,使得 ,则点A的横坐标的取值范围是 .
,则点A的横坐标的取值范围是 . (
( 、
、 ),满足
),满足 ,且
,且 在
在 时恒成立.
时恒成立. 的值;
的值; ,解不等式
,解不等式 ;
; ,使函数
,使函数 在区间
在区间 上有最小值
上有最小值 ?若存在,请求出
?若存在,请求出 粤公网安备 44130202000953号
粤公网安备 44130202000953号