已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则( )
| A.α∥β且l∥α |
| B.α⊥β且l⊥β |
| C.α与β相交,且交线垂直于l |
| D.α与β相交,且交线平行于l |
在正方体ABCD-A1B1C1D1中,E,F分别为棱AA1,CC1的中点,则在空间中与三条直线A1D1,EF,CD都相交的直线( )
| A.不存在 | B.有且只有两条 |
| C.有且只有三条 | D.有无数条 |
已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为( )
| A.16π | B.24π | C.32 π π |
D.48π |
已知m,n是空间两条不同的直线,α,β,γ是三个不同的平面,则下列命题中为真的是( )
| A.若α∥β,m⊂α,n⊂β,则m∥n |
| B.若α∩γ=m,β∩γ=n,m∥n,则α∥β |
| C.若m⊂β,α⊥β,则m⊥α |
| D.若m⊥β,m∥α,则α⊥β |
设m,n是两条不同的直线,α,β是两个不同的平面.则下列结论中正确的是( )
| A.若m∥α,n∥α,则m∥n |
| B.若m∥α,m∥β,则α∥β |
| C.若m∥n,m⊥α,则n⊥α |
| D.若m∥α,α⊥β,则m⊥β |
设 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题:
(1)若 ,则
,则 ;
;
(2)若

 ,
,

 ,
, ,则
,则 ;
;
(3)若 ,
,

 ,则
,则 ;
;
(4)若 ,
, ,
, ,
, ,则
,则 .
.
其中正确的命题是( )
| A.(1)(3) | B.(2)(3) |
| C.(2)(4) | D.(3)(4) |
已知集合 且
且 ={直线},
={直线}, ={平面},
={平面}, ,若
,若 ,有四个命题①
,有四个命题① ②
② ③
③ ④
④ 其中所有正确命题的序号是( )
其中所有正确命题的序号是( )
| A.①②③ | B.②③④ | C.②④ | D.④ |
如图,在正方形ABCD中,E、F分别是BC、CD的中点,AC∩EF=G.现在沿AE、EF、FA把这个正方形折成一个四面体,使B、C、D三点重合,重合后的点记为P,则在四面体P-AEF中必有 ( ).
| A.AP⊥△PEF所在平面 |
| B.AG⊥△PEF所在平面 |
| C.EP⊥△AEF所在平面 |
| D.PG⊥△AEF所在平面 |
下列命题中错误的是 ( ).
| A.如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β |
| B.如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β |
| C.如果平面α⊥平面γ,平面β⊥平面γ,α∩β=l,那么l⊥平面γ |
| D.如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β |
已知正方体 ,点
,点 ,
, ,
, 分别是线段
分别是线段 ,
, 和
和 上的动点,观察直线
上的动点,观察直线 与
与 ,
, 与
与 .给出下列结论:
.给出下列结论:
①对于任意给定的点 ,存在点
,存在点 ,使得
,使得
 ;
;
②对于任意给定的点 ,存在点
,存在点 ,使得
,使得
 ;
;
③对于任意给定的点 ,存在点
,存在点 ,使得
,使得
 ;
;
④对于任意给定的点 ,存在点
,存在点 ,使得
,使得
 .
.
其中正确结论的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
已知直线 ,平面
,平面 .则“
.则“ ”是“
”是“ 直线
直线 ,
, ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知 表示一条直线,
表示一条直线, ,
, 表示两个不重合的平面,有以下三个语句:①
表示两个不重合的平面,有以下三个语句:① ;②
;② ;③
;③ .以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
A. |
B. |
C. |
D. |
四棱锥P-ABCD中,底面ABCD是平行四边形,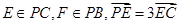 ,
,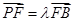 ,若
,若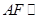 平面BDE,则
平面BDE,则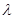 的值为 ( )
的值为 ( )
| A.1 | B.3 | C.2 | D.4 |
如图,正方体 的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线 上,过点P作垂直于
上,过点P作垂直于 的平面
的平面 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设 x,则当
x,则当 时,函数
时,函数 的值域为( )
的值域为( )
A. |
B. |
C. |
D. |
设 、
、 是两条不同的直线,
是两条不同的直线,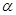 、
、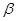 是两个不同的平面.下列四个命题中,正确的是( )
是两个不同的平面.下列四个命题中,正确的是( )
A.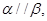 , ,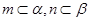 ,则 ,则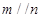 |
B.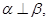 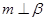 ,则 ,则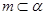 |
C.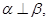 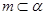 , ,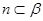 ,则 ,则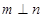 |
D.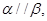 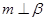 , , ,则 ,则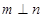 |