[北京]2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
“ ”是“直线
”是“直线 与圆
与圆 相切”的( )
相切”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
已知 表示一条直线,
表示一条直线, ,
, 表示两个不重合的平面,有以下三个语句:①
表示两个不重合的平面,有以下三个语句:① ;②
;② ;③
;③ .以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
.以其中任意两个作为条件,另外一个作为结论,可以得到三个命题,其中正确命题的个数是( )
A. |
B. |
C. |
D. |
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
 ,
, 是两个不重合的平面,在下列条件中,可判定
是两个不重合的平面,在下列条件中,可判定 ∥
∥ 的是( )
的是( )
A. , , 都与平面 都与平面 垂直 垂直 |
B. 内不共线的三点到 内不共线的三点到 的距离相等 的距离相等 |
C. , , 是 是 内的两条直线且 内的两条直线且 ∥ ∥ , , ∥ ∥ |
D. , , 是两条异面直线且 是两条异面直线且 ∥ ∥ , , ∥ ∥ , , ∥ ∥ , ,  ∥ ∥ |
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
已知抛物线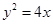 的准线与双曲线
的准线与双曲线 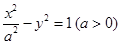 交于
交于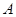 ,
, 两点,点
两点,点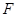 为抛物线的焦点,若△
为抛物线的焦点,若△ 为直角三角形,则
为直角三角形,则 的值为( )
的值为( )
A. |
B.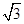 |
C. |
D.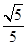 |
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
正方体 中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 到平面
到平面 的距离是
的距离是 到直线
到直线 距离的
距离的 倍,则动点
倍,则动点 的轨迹为( )
的轨迹为( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.圆 |
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为 的两个全等的等腰直角三角形,则这个几何体的体积为 .
的两个全等的等腰直角三角形,则这个几何体的体积为 .
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
过椭圆 的左顶点
的左顶点 的斜率为
的斜率为 的直线交椭圆于另一个点
的直线交椭圆于另一个点 ,且点
,且点 在
在 轴上的射影恰好为右焦点
轴上的射影恰好为右焦点 ,若
,若 ,则椭圆离心率的取值范围是_____________.
,则椭圆离心率的取值范围是_____________.
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
已知圆 的圆心在直线
的圆心在直线 上,且与
上,且与 轴交于两点
轴交于两点 ,
, .
.
(1)求圆 的方程;
的方程;
(2)求过点
 的圆
的圆 的切线方程;
的切线方程;
(3)已知 ,点
,点 在圆
在圆 上运动,求以
上运动,求以 ,
, 为一组邻边的平行四边形的另一个顶点
为一组邻边的平行四边形的另一个顶点 轨迹方程.
轨迹方程.
来源:2013-2014学年北京东城区高二第一学期期末考试理科数学试卷
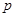 :
: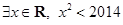 ,则
,则 为( )
为( )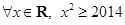


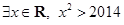
 在
在 轴上的截距为( )
轴上的截距为( )



 的渐近线方程为( )
的渐近线方程为( )



 ,
, ,
, 的斜率分别为
的斜率分别为 ,
, ,
, ,则( )
,则( )
 ,则椭圆
,则椭圆 的离心率是( )
的离心率是( )


 的取值有关
的取值有关 ,
, ,且
,且 ,那么
,那么 等于( )
等于( )



 中,与
中,与 所在直线所成的角为
所在直线所成的角为 是( )
是( )



 过圆
过圆 的圆心,则
的圆心,则 的值为 .
的值为 . 与直线
与直线 互相垂直,则
互相垂直,则 的值为 .
的值为 . ,
, 是椭圆
是椭圆 的左、右焦点,过
的左、右焦点,过 ,
, 两点,若
两点,若 的周长为
的周长为 ,则
,则 的值为 .
的值为 . 与圆
与圆 相交于
相交于 ,
, 两点,且
两点,且 (其中
(其中 为原点),则
为原点),则 的值为 .
的值为 . 平面
平面 ,
, ,
, ,
, 为
为 的中点.
的中点.
 平面
平面
 平面
平面 .
. 与
与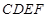 均为正方形,平面
均为正方形,平面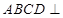 平面
平面
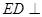 平面
平面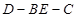 的大小.
的大小. :
: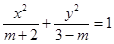
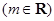 .
.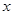 轴上的椭圆,求
轴上的椭圆,求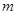 的取值范围;
的取值范围; ,过点
,过点 的直线
的直线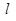 与曲线
与曲线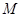 ,
, 两点,
两点,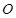 为坐标原点,若
为坐标原点,若 为直角三角形,求直线
为直角三角形,求直线 粤公网安备 44130202000953号
粤公网安备 44130202000953号