[北京]2014届北京市西城区高三上学期期末考试理科数学试卷
已知圆 与x轴切于A点,与y轴切于B点,设劣弧
与x轴切于A点,与y轴切于B点,设劣弧 的中点为M,则过点M的圆C的切线方程是( )
的中点为M,则过点M的圆C的切线方程是( )
A. |
B. |
C. |
D. |
如图,正方体 的棱长为
的棱长为 ,动点P在对角线
,动点P在对角线 上,过点P作垂直于
上,过点P作垂直于 的平面
的平面 ,记这样得到的截面多边形(含三角形)的周长为y,设
,记这样得到的截面多边形(含三角形)的周长为y,设 x,则当
x,则当 时,函数
时,函数 的值域为( )
的值域为( )
A. |
B. |
C. |
D. |
已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为______.
甲、乙两名大学生从4个公司中各选2个作为实习单位,则两人所选的实习单位中恰有1个相同的选法种数是______.(用数字作答)
在平面直角坐标系 中,记不等式组
中,记不等式组 所表示的平面区域为
所表示的平面区域为 .在映射
.在映射 的作用下,区域
的作用下,区域 内的点
内的点 对应的象为点
对应的象为点 .
.
(1)在映射 的作用下,点
的作用下,点 的原象是 ;
的原象是 ;
(2)由点 所形成的平面区域的面积为______.
所形成的平面区域的面积为______.
以下茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以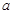 表示.
表示.
(Ⅰ)若甲、乙两个小组的数学平均成绩相同,求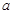 的值;
的值;
(Ⅱ)求乙组平均成绩超过甲组平均成绩的概率;
(Ⅲ)当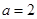 时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为
时,分别从甲、乙两组中各随机选取一名同学,记这两名同学数学成绩之差的绝对值为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形, ,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
(Ⅰ)求证:AC⊥平面BDEF;
(Ⅱ)求直线DH与平面 所成角的正弦值;
所成角的正弦值;
(Ⅲ)求二面角 的大小.
的大小.
已知函数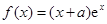 ,其中
,其中 是自然对数的底数,
是自然对数的底数,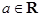 .
.
(Ⅰ)求函数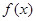 的单调区间;
的单调区间;
(Ⅱ)当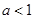 时,试确定函数
时,试确定函数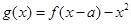 的零点个数,并说明理由.
的零点个数,并说明理由.
已知 是抛物线
是抛物线 上的两个点,点
上的两个点,点 的坐标为
的坐标为 ,直线
,直线 的斜率为k,
的斜率为k,  为坐标原点.
为坐标原点.
(Ⅰ)若抛物线 的焦点在直线
的焦点在直线 的下方,求k的取值范围;
的下方,求k的取值范围;
(Ⅱ)设C为W上一点,且 ,过
,过 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为 ,求
,求 的最小值.
的最小值.
 ,
, ,则集合
,则集合 ( )
( )



 ,那么
,那么 的虚部为( )
的虚部为( )



 ,
, ,
, ,则
,则 ( )
( )








 为焦点在
为焦点在 轴上的椭圆,则实数
轴上的椭圆,则实数 ,
, 满足( )
满足( )



 满足
满足 ,且当
,且当 时,
时, ,则当
,则当 时,
时,



 中,点
中,点 ,
, ,若向量
,若向量 ,则实数
,则实数 _____.
_____. 满足
满足 ,
, ,则公差
,则公差 ______;
______; ______.
______. 为圆
为圆 上的两个点,
上的两个点, 为
为 延长线上一点,
延长线上一点, 为圆
为圆 为切点. 若
为切点. 若 ,
, ,则
,则 ______;
______; ______.
______.
 ,
, ,且
,且 的最小正周期为
的最小正周期为 .
. ,
, ,求
,求 的值;
的值; 的单调增区间.
的单调增区间. 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数 的最大整数(如
的最大整数(如 ),记
),记 ,数列
,数列 项和为
项和为 ,数列
,数列 的前
的前 .
. ,求
,求 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
. (
( )的充分必要条件为
)的充分必要条件为 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号