在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1) 证明: ;
;
(2) 证明: 平面
平面 ;
;
(3) 求二面角 的余弦值.
的余弦值.
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,且分别交AC、PC于D、E两点,又PB=BC,PA=AB。
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,并证明你的结论;
(3)若AB=2,求三棱锥B-CED的体积
已知直线 ,平面
,平面 ,且
,且 ,
, ,给出下列四个命题:
,给出下列四个命题:
①若 ∥
∥ ,则
,则 ;②若
;②若 ,则
,则 ∥
∥ ;
;
③若 ,则
,则 ∥
∥ ;④若
;④若 ∥
∥ ,则
,则 ;
;
其中为真命题的序号是_______
下列命题中,真命题是( )
A.若直线m、n都平行于 ,则 ,则 |
B.设 是直二面角,若直线 是直二面角,若直线 则 则 |
C.若 在平面 在平面 内的射影依次是一个点和一条直线,且 内的射影依次是一个点和一条直线,且 ,则 ,则 或 或 |
D.若直线m、n是异面直线,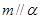 ,则n与 ,则n与 相交 相交 |
正方体ABCD-A1B1C1D1中,E为A1C1的中点,则直线CE垂直于 ( )
| A.直线AC | B.直线B1D1 |
| C.直线A1D1 | D.直线A1A |
设 ,
, 是两条不同的直线,
是两条不同的直线, ,
, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , ,则 ,则 ; ; |
B.若 , , ,则 ,则 ; ; |
C.若 , , , , ,则 ,则 ; ; |
D.若 , , , , ,则 ,则 . . |
设 是不同的直线,
是不同的直线, 是不同的平面,则下列结论错误的是( )
是不同的平面,则下列结论错误的是( )
A.若 则 则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
关于直线 与平面
与平面 有以下三个命题
有以下三个命题
⑴若
⑵若
⑶若 ,其中真命题有
,其中真命题有
| A.1个 | B.2个 | C.3个 | D.0个 |
如图所示的七面体是由三棱台ABC – A1B1C1和四棱锥D- AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面ABCD,BB1=2A1B1=2.
(I)求证:平面AA1C1C1⊥平面BB1D;
(Ⅱ)求二面角A –A1D—C1的余弦值.
如图:C、D是以AB为直径的圆上两点, 在线段
在线段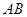 上,且
上,且 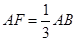 ,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.
,将圆沿直径AB折起,使点C在平面ABD的射影E在BD上.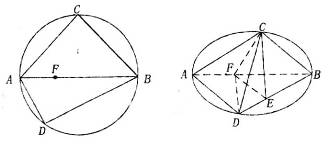
(I)求证平面ACD⊥平面BCD;
(II)求证:AD//平面CEF.
给出下列四个命题:
①垂直于同一平面的两条直线相互平行; ②垂直于同一平面的两个平面相互平行;
③若一个平面内有无数条直线与另一个平面都平行,那么这两个平面相互平行;
④若一条直线垂直于一个平面内的任一直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |