[甘肃]2012年高考预测系列试题(数学)高考预测试卷(7)
设 则“
则“ 且
且 ”是“
”是“ ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.即不充分也不必要条件 |
执行右面的程序框图,如果输入的N是5,那么输出的S是 ( )
| A.-385 | B.-399 | C.-45. | D.-55 |
定义新运算“ ”:当a≥b时,a
”:当a≥b时,a b=a;当a<b时,a
b=a;当a<b时,a b=b2,则函数f(x)=(1
b=b2,则函数f(x)=(1 x)x-(2
x)x-(2 x),x∈[-2,2]的最大值等于( )
x),x∈[-2,2]的最大值等于( )
| A.-1 | B.1 | C.6 | D.12 |
使方程x5-3x-1=0至少有一个实根的区间不可能是( )
| A.(-2,-1) | B.(-1,1) | C.(1,2) | D.(2,3) |
设D、E、F分别是△ABC的三边BC、CA、AB上的点,且

 则
则 与
与 ( )
( )
A、反向平行 B、同向平行
C、互相垂直 D、既不平行也不垂直
设双曲线 的半焦距为c,直线l过
的半焦距为c,直线l过 两点,若原点O到l的距离为
两点,若原点O到l的距离为 则双曲线的离心率为( )
则双曲线的离心率为( )
A. 或2 或2 |
B.2 | C. 或 或 |
D. |
给出下列四个命题:
①垂直于同一平面的两条直线相互平行; ②垂直于同一平面的两个平面相互平行;
③若一个平面内有无数条直线与另一个平面都平行,那么这两个平面相互平行;
④若一条直线垂直于一个平面内的任一直线,那么这条直线垂直于这个平面.
其中真命题的个数是( )
| A.1个 | B.2个 | C.3个 | D.4个 |
如图,点ABC都在⊙O上,过点C的切线交AB的延长线于点D,若AB=5,BC=3,CD=6,则线段AC的长为 ( )
A. |
B. |
C. |
D. |

四棱锥 的底面
的底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)证明 //平面
//平面 ;
;
(Ⅱ)求二面角 的平面角的余弦值;
的平面角的余弦值;
(Ⅲ)在棱 上是否存在点
上是否存在点 ,使
,使 ⊥平面
⊥平面 ?若存在,请求出
?若存在,请求出 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.
已知函数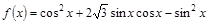 .
.
(1)求函数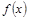 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(2)需要把函数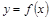 的图像经过怎样的变换才能得到函数
的图像经过怎样的变换才能得到函数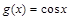 的图像?
的图像?
(3)在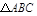 中,
中,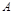 、
、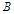 、
、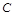 分别为三边
分别为三边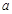 、
、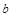 、
、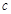 所对的角,若
所对的角,若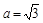 ,
,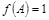 ,求
,求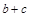 的最大值.
的最大值.
.已知方向向量为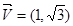 的直线l过椭圆
的直线l过椭圆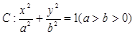 的焦点以及点(0,
的焦点以及点(0,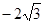 ),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为
),直线l与椭圆C交于 A 、B两点,且A、B两点与另一焦点围成的三角形周长为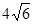 .
.
(1)求椭圆C的方程;
(2)过左焦点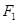 且不与x轴垂直的直线m交椭圆于M、N两点,
且不与x轴垂直的直线m交椭圆于M、N两点, 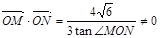 (O坐标原点),求直线m的方程.
(O坐标原点),求直线m的方程.
 ,
, ,则
,则




 ,
, ,则
,则 ,
, B、
B、 ,
, D、
D、 、
、 满足
满足 ,则有 ( )
,则有 ( ) ;
; ;
; ;
; .
. }的前
}的前 项和为
项和为 ,且
,且 ,
, ,则
,则 为( )
为( )



 满足不等式组
满足不等式组 ,目标函数
,目标函数 .若取最大值时的唯一最优解是(1,3),则实数
.若取最大值时的唯一最优解是(1,3),则实数 的取值范围是 .
的取值范围是 . f(x)dx=2f(a)成立,则a=________.
f(x)dx=2f(a)成立,则a=________. 外一点
外一点 分别作圆的切线和割线交圆于
分别作圆的切线和割线交圆于 ,且
,且 ,
, 是圆上一点使得
是圆上一点使得 ,
, ,则
,则 ___________.
___________.
 与
与 的交点的极坐标为______.
的交点的极坐标为______. 的前n项和,且
的前n项和,且
 ,是否存在最大的正整数k,使得对于任意的正整数n,有
,是否存在最大的正整数k,使得对于任意的正整数n,有 恒成立?若存在,求出k的值;若不存在,说明理由.
恒成立?若存在,求出k的值;若不存在,说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号