高中数学随机事件试题

一个篮球运动员投篮一次得3分的概率为，得2分的概率为，不得分的概率为（、、），已知他投篮一次得分的数学期望为2（不计其它得分情况），则的最大值为（　　）

A．

B．

C．

D．

某射手进行射击训练，假设每次射击击中目标的概率为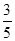，且每次射击的结果互不影响，已知射手射击了5
次，求：
(1)其中只在第一、三、五次击中目标的概率；
(2)其中恰有3次击中目标的概率．

为了解某校学生的视力情况，现采用随机抽样的方式从该校的A，B两班中各抽5名学生进行视力检测．检测的数据如下：
A班5名学生的视力检测结果：4.3，5.1，4.6，4.1，4.9.
B班5名学生的视力检测结果：5.1，4.9，4.0，4.0，4.5.
（1）分别计算两组数据的平均数，从计算结果看，哪个班的学生视力较好？；
（2）由数据判断哪个班的5名学生视力方差较大？（结论不要求证明）
（3）根据数据推断A班全班40名学生中有几名学生的视力大于4.6？

小王参加一次比赛，比赛共设三关，第一、二关各有两个必答题，如果每关两个问题都答对，可进入下一关，第三关有三个问题，只要答对其中两个问题，则闯关成功．每过一关可一次性获得价值分别为1000元，3000元，6000元的奖品(不重复得奖)，小王对三关中每个问题回答正确的概率依次为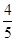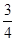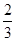，，，且每个问题回答正确与否相互独立．
(1)求小王过第一关但未过第二关的概率；
(2)用X表示小王所获得奖品的价值，写出X的概率分布列，并求X的数学期望．

在高三的一个班中，有的学生数学成绩优秀，若从班中随机找出5名学生，那么数学成绩优秀的学生数ξ～B(5，)，则P(ξ＝k)取最大值的k值为(　　)

A．0

B．1

C．2

D．3

在15个村庄中有7个村庄交通不便，现从中任意选10个村庄，用ξ表示这10个村庄中交通不便的村庄数，下列概率中等于的是(　　)

A．P(ξ＝2)	B．P(ξ≤2)
C．P(ξ＝4)	D．P(ξ≤4)

在不等式组所表示的平面区域内的所有格点(横、纵坐标均为整数的点称为格点)中任取3个点，则该3点恰能作为一个三角形的3个顶点的概率为________．

甲、乙两人一起去游玩，他们约定各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后1小时他们在同一个景点的概率是(　　)

A．

B．

C．

D．

如图所示的茎叶图表示的是甲、乙两人在五次综合测评中的成绩，其中一个数字被污损，则甲的平均成绩不超过乙的平均成绩的概率为(　　)

A．

B．

C．

D．

5张卡片上分别写有数字1,2,3,4,5，从这5张卡片中随机抽取2张，则取出2张卡片上数字之和为偶数的概率为(　　)

A．

B．

C．

D．

掷一枚均匀的硬币两次，事件M：一次正面朝上，一次反面朝上，事件N：至少一次正面朝上，则下列结果正确的是(　　)

A．P(M)＝，P(N)＝	B．P(M)＝，P(N)＝
C．P(M)＝，P(N)＝	D．P(M)＝，P(N)＝

某工艺厂开发一种新工艺品，头两天试制中，该厂要求每位师傅每天制作10件，该厂质检部每天从每位师傅制作的10件产品中随机抽取4件进行检查，若发现有次品，则当天该师傅的产品不能通过．已知李师傅第一天、第二天制作的工艺品中分别有2件、1件次品．
(1)求两天中李师傅的产品全部通过检查的概率；
(2)若厂内对师傅们制作的工艺品采用记分制，两天都不通过检查的得0分，两天中只通过一天检查的得1分，两天都通过检查的得2分，求李师傅在这两天内得分的数学期望．

一个盒子里装有三张卡片，分别标记有数字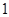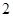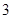，，，这三张卡片除标记的数字外完全相同。随机有放回地抽取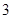次，每次抽取张，将抽取的卡片上的数字依次记为.
（Ⅰ）求"抽取的卡片上的数字满足"的概率；
（Ⅱ）求"抽取的卡片上的数字不完全相同"的概率.

[2013·课标全国卷Ⅱ]从1,2,3,4,5中任意取出两个不同的数，其和为5的概率是________．

已知箱子里装有4张大小、形状都相同的卡片，标号分别为1,2,3,4．
（1）从箱子中任取两张卡片，求两张卡片的标号之和不小于5的概率；
（2）从箱子中任意取出一张卡片，记下它的标号，然后再放回箱子中；第二次再从箱子中任取一张卡片，记下它的标号，求使得幂函数图像关于轴对称的概率．