假设关于某种设备的使用年限 和支出的维修费用
和支出的维修费用 (万元),有以下的统计资料:
(万元),有以下的统计资料:
使用年限 |
2 |
3 |
4 |
5 |
6 |
维修费用 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
(1)求支出的维修费用 与使用年限
与使用年限 的线性回归方程;
的线性回归方程;
(2)估计使用年限为10年时,维修费用是多少?
( )
)
一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归直线方程为 ,据此可以预测这个孩子10岁时的身高,则正确的叙述是
,据此可以预测这个孩子10岁时的身高,则正确的叙述是
| A.身高一定是145.83cm | B.身高超过146.00cm |
| C.身高低于145.00cm | D.身高在145.83cm左右 |
观察两个相关变量的如下数据:
 |
-1 |
-2 |
-3 |
-4 |
-5 |
5 |
4 |
3 |
2 |
1 |
 |
-0.9 |
-2 |
-3.1 |
-3.9 |
-5.1 |
5 |
4.1 |
2.9 |
2.1 |
0.9 |
则两个变量间的回归直线方程为 ( )
A. |
B. |
C. |
D.  |
工人工资(元)依劳动生产率(千元)变化的回归方程为y=50+80x,下列判断中正确的是
| A.劳动生产率为1000元时,工资为130元 |
| B.劳动生产率平均提高1000元时,工资平均提高80元 |
| C.劳动生产率平均提高1000元时,工资平均提高130元 |
| D.当工资为250元时,劳动生产率为2000元 |
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为 万元,
万元, 万元,农民得到的补贴为
万元,农民得到的补贴为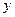 万元,解答以下问题.
万元,解答以下问题.
| |
A型号 |
B型号 |
| 电视机价值(万元) |
 |
 |
| 农民获得补贴(万元) |
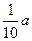 |
 |
(1) 用 的代数式表示
的代数式表示
(2) 当 取何值时,
取何值时, 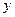 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: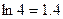 )
)
某设备的使用年限 与所支出的维修费用
与所支出的维修费用 (万元)有左下表统计资料.若由资料知
(万元)有左下表统计资料.若由资料知 对
对 呈线性相关关系,则线性回归方程为
呈线性相关关系,则线性回归方程为 ﹡ .
﹡ .
 |
2 |
3 |
4 |
5 |
6 |
 |
2 |
4 |
6 |
6 |
7 |
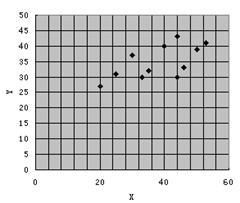
某次数学测试分为选择题与非选择题两部分,
右边的散点图中每个点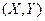 表示一位学生在
表示一位学生在
这两部分的得分,其中 表示该生选择题得
表示该生选择题得
分, 表示该生非选择题得分,设
表示该生非选择题得分,设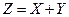 表
表
示该生的总分,现有11位学生的得分数据,根
据散点图,下列判断正确的是( )
A. 的方差< 的方差< 的方差 的方差 |
B. 的中位数> 的中位数> 的中位数 的中位数 |
C. 的众数< 的众数< 的众数 的众数 |
D.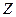 的中位数= 的中位数= 的中位数+ 的中位数+ 的中位数 的中位数 |
体育课上,八年级一班两个组各10人参加立定跳远,要判断哪一组成绩比较整齐,通常需要知道这两个组立定跳远成绩的( )
| A.频率分布 | B.平均数 | C.方差 | D.众数 |
12分)某个服装店经营某种服装,在某周内获纯利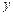 (元),与该周每天销售这种服装件数
(元),与该周每天销售这种服装件数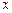 之间的一组数据关系见表:
之间的一组数据关系见表:
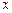 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
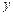 |
66 |
69 |
73 |
81 |
89 |
90 |
91 |
已知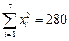 ,
,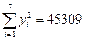 ,
,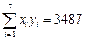 .
.
(1)求 ;
;
(2)画出散点图;
(3)求出回归方程.
(参考公式: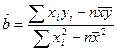
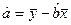 )
)
为调查吸烟是否对患肺癌有影响,某肿瘤研究所随机地调查了50人,得到如下结果(单位:人)
| |
不患肺癌 |
患肺癌 |
合计 |
| 不吸烟 |
24 |
6 |
30 |
| 吸烟 |
6 |
14 |
20 |
| 合计 |
30 |
20 |
50 |
根据表中数据,你认为吸烟与患肺癌有关的把握有
A  B
B  C
C  D
D 
对于散点图下列说法中正确一个是
A通过散点图一定可以看出变量之间的变化规律
B通过散点图一定不可以看出变量之间的变化规律
C通过散点图可以看出正相关与负相关有明显区别
D通过散点图看不出正相关与负相关有什么区别