广东省广州市七区联考高二数学(文)下学期期末监测
复数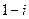 在复平面内对应的点位于( ﹡ ).
在复平面内对应的点位于( ﹡ ).
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
若大前提是:任何实数的平方都大于0,小前提是: ,结论是:
,结论是: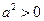 ,那么这个演绎推理所得结论错误的原因是:( ﹡ ).
,那么这个演绎推理所得结论错误的原因是:( ﹡ ).
| A.大前提错误 | B.小前提错误 | C.推理形式错误 | D.大前提小前提都错 |
若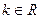 ,则
,则 是方程
是方程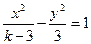 表示双曲线的( ﹡ ).
表示双曲线的( ﹡ ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
甲、乙、丙、丁四位同学各自对A、B两变量的线性相关性作试验,并用回归分析方法分别求得相关系数r与残差平方和m如下表;则哪位同学的试验结果体现A、B两变量更强的线性相关性
A.丁 B.丙 C.乙 D.甲
| |
甲 |
乙 |
丙 |
丁 |
| r |
0.82 |
0.78 |
0.69 |
0.85 |
| m |
115 |
106 |
124 |
103 |
下列各图是由一些火柴棒拼成的一系列图形,如第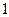 个图中有
个图中有 根火柴棒,第
根火柴棒,第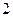 个图中有
个图中有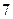 根火柴棒,则在第
根火柴棒,则在第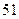 个图中有火柴棒( ﹡ ).
个图中有火柴棒( ﹡ ). 
A. 根 根 |
B. 根 根 |
C. 根 根 |
D. 根 根 |
已知四个命题:① 使
使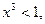 ②
②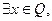 使
使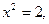 ③
③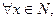 有
有 ④
④ 有
有 .其中的真命题是:( ﹡ )
.其中的真命题是:( ﹡ )
| A.①④ | B.②③ | C.①③ | D.②④ |
已知函数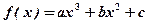 ,其导函数图象如图1所示,
,其导函数图象如图1所示,
则函数 的极小值是 ( * )
的极小值是 ( * ) 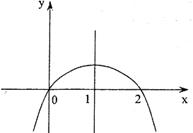
A. |
B.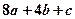 |
C.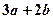 |
D.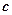 |
已知椭圆 的离心率
的离心率 ,过左焦点
,过左焦点 的直线交椭圆于
的直线交椭圆于 两点,椭圆的右焦点为
两点,椭圆的右焦点为 ,则
,则 的周长是 ﹡ .则可以输出的函数是 ﹡ .
的周长是 ﹡ .则可以输出的函数是 ﹡ .
某设备的使用年限 与所支出的维修费用
与所支出的维修费用 (万元)有左下表统计资料.若由资料知
(万元)有左下表统计资料.若由资料知 对
对 呈线性相关关系,则线性回归方程为
呈线性相关关系,则线性回归方程为 ﹡ .
﹡ .
 |
2 |
3 |
4 |
5 |
6 |
 |
2 |
4 |
6 |
6 |
7 |
(本小题满分12分)
先阅读以下不等式的证明,再类比解决后面的问题
若 ,则
,则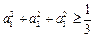 .
.
证明:构造二次函数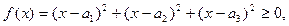
将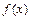 展开得:
展开得: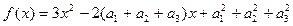

 对一切实数
对一切实数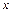 恒有
恒有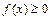 ,且抛物线的开口向上
,且抛物线的开口向上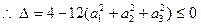 ,
, .
.
(Ⅰ)类比猜想:
若 ,则 .
,则 .
(在横线上填写你的猜想结论)
(Ⅱ)证明你的猜想结论.
(本小题满分14分)
如图,四边形 为矩形,
为矩形, 且
且 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面
(1)设点 为线段
为线段 的中点,点
的中点,点 为线段
为线段 的中点,求证:
的中点,求证: ∥平面
∥平面

(2)求证 

(3)当 时,求三棱锥
时,求三棱锥 的体积。
的体积。
(本小题满分14分)
为积极响应国家“家电下乡”政策的号召,某厂家把总价值为10万元的A、B两种型号的电视机投放市场,并且全部被农民购买。若投放的A、B两种型号的电视机价值都不低于1万元,农民购买A、B两种型号的电视机将按电视机价值的一定比例给予补贴,补贴方案如下表所示,设投放市场的A、B型号电视机的价值分别为 万元,
万元, 万元,农民得到的补贴为
万元,农民得到的补贴为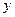 万元,解答以下问题.
万元,解答以下问题.
| |
A型号 |
B型号 |
| 电视机价值(万元) |
 |
 |
| 农民获得补贴(万元) |
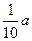 |
 |
(1) 用 的代数式表示
的代数式表示
(2) 当 取何值时,
取何值时, 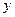 取最大值并求出其最大值(精确到0.1,参考数据:
取最大值并求出其最大值(精确到0.1,参考数据: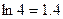 )
)
(本小题满分14分)
已知函数 ,
, 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
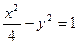 的焦点坐标为( ﹡ ).
的焦点坐标为( ﹡ ). 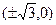

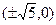

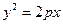 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则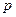 的值为( ﹡ )
的值为( ﹡ )
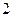

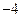
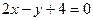 平行的抛物线
平行的抛物线 的切线方程为( ﹡ )
的切线方程为( ﹡ ) 

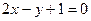
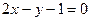
 的准线方程是 ﹡ .
的准线方程是 ﹡ . 的单调递减区间是 ﹡ .
的单调递减区间是 ﹡ . 中,已知
中,已知 ,且
,且 .
.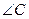 的大小。
的大小。 过椭圆C:
过椭圆C: 的右焦点F,
的右焦点F, 上的射影依次为点D、E.
上的射影依次为点D、E.
 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程; 为x轴上一点;
为x轴上一点; 粤公网安备 44130202000953号
粤公网安备 44130202000953号