上海市普陀区高三数学高考临考自测练习卷
从某批灯泡中随机抽取10只做寿命试验,其寿命(以小时计)如下:
1050,1100,1120,1280,1250,1040,1030,1110,1240,1300.则该批灯泡寿命标准差的点估计值等于 .(结果保留一位小数)
理)如图,正四面体 的顶点
的顶点 ,
, ,
, 分别在两两垂直的三条射线
分别在两两垂直的三条射线 ,
, ,
, 上,则在下列命题中,正确命题的个数为_______.
上,则在下列命题中,正确命题的个数为_______.
(1) 是正三棱锥 ;
是正三棱锥 ;
(2)直线 ∥平面
∥平面 ;
;
(3)直线 与
与 所成的角是
所成的角是 ;
;
(4)二面角 为
为 .
.
体育课上,八年级一班两个组各10人参加立定跳远,要判断哪一组成绩比较整齐,通常需要知道这两个组立定跳远成绩的( )
| A.频率分布 | B.平均数 | C.方差 | D.众数 |
在100个零件中,有一级品20个,二级品30个,三级品50个,从中抽取20个作为样本:①采用随机抽样法,将零件编号为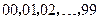 ,抽出20个;②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;③采用分层抽样法,随机从一级品中抽取4个,二级品中抽取6个,三级品中抽取10个;则( )
,抽出20个;②采用系统抽样法,将所有零件分成20组,每组5个,然后每组中随机抽取1个;③采用分层抽样法,随机从一级品中抽取4个,二级品中抽取6个,三级品中抽取10个;则( )
A.不论采取哪种抽样方法,这100个零件中每个被抽到的概率都是 |
B.①②两种抽样方法,这100个零件中每个被抽到的概率都是 ,③并非如此 ,③并非如此 |
C.①③两种抽样方法,这100个零件中每个被抽到的概率都是 ,②并非如此 ,②并非如此 |
| D.采用不同的抽样方法,这100个零件中每个被抽到的概率各不相同 |
(理)袋中有同样的球 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机且不返回地摸球,每次摸
个黄色,现从中随机且不返回地摸球,每次摸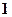 个,当两种颜色的球都被摸到时,即停止摸球,记随机变量
个,当两种颜色的球都被摸到时,即停止摸球,记随机变量 为此时已摸球的次数,求:.
为此时已摸球的次数,求:.
(1)随机变量 的概率分布律;
的概率分布律;
(2)随机变量 的数学期望与方差.
的数学期望与方差.
(文)袋中有同样的球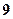 个,其中
个,其中 个红色,
个红色, 个黄色,现从中随机地摸
个黄色,现从中随机地摸 球,求:
球,求:
(1)红色球与黄色球恰好相等的概率(用分数表示结果)
(2)红色球多于黄色球的不同摸法的和数.
杨辉是中国南宋末年的一位杰出的数学家、数学教育家. 杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.下图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为 ,求n的值;
,求n的值;
(3)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k 的数学公式表示上述结论,并给予证明.
的数学公式表示上述结论,并给予证明. 
(理)已知等差数列 的公差是
的公差是 ,
, 是该数列的前
是该数列的前 项和.
项和.
(1)试用 表示
表示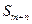 ,其中
,其中 、
、 均为正整数;
均为正整数;
(2)利用(1)的结论求解:“已知
 ,求
,求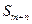 ”;
”;
(3)若数列 前
前 项的和分别为
项的和分别为
 ,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列
,试将问题(1)推广,探究相应的结论. 若能证明,则给出你的证明并求解以下给出的问题;若无法证明,则请利用你的研究结论和另一种方法计算以下给出的问题,从而对你猜想的可靠性作出自己的评价.问题:“已知等差数列 的前
的前 项和
项和 ,前
,前 项和
项和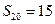 ,求数列
,求数列 的前2010项的和
的前2010项的和 .”
.”
 ,
, ,则向量
,则向量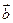 在
在 上的投影为_________.
上的投影为_________. 中第二行第一列元素0的代数余子式是________.
中第二行第一列元素0的代数余子式是________. 的增广矩阵是_________________.
的增广矩阵是_________________. 、
、 ,若
,若 ,则直线
,则直线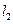 的一个方向向量为
的一个方向向量为 .
. 与圆
与圆 的交点坐标是__________.
的交点坐标是__________. 满足条件
满足条件 并使
并使 取得最大值时P点的坐标是____
取得最大值时P点的坐标是____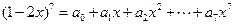 ,
, __________.
__________. 无实数根;命题Q:不等式
无实数根;命题Q:不等式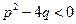 .则命题P与命题Q的推出关系是____________.
.则命题P与命题Q的推出关系是____________.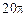 ,且母线与底面所成的角为
,且母线与底面所成的角为 ,则该圆锥的体积为______.
,则该圆锥的体积为______.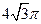 的球面上有
的球面上有 三点,
三点, ,
, ,
, 两点的球面距离为
两点的球面距离为 ,则球心到平面
,则球心到平面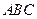 的距离为_______________.
的距离为_______________.
 在区间
在区间 上有零点,则所有满足条件的
上有零点,则所有满足条件的 的值的和为 ______.
的值的和为 ______.


 =(1,1),
=(1,1), =(-1,1),
=(-1,1),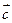 =(4,2),则向量
=(4,2),则向量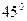 、腰和上底均为1的等腰梯形,那么原平面图形的面积为( )
、腰和上底均为1的等腰梯形,那么原平面图形的面积为( )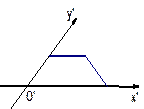




 ,并对解的情况进行讨论.
,并对解的情况进行讨论.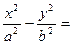 1的右焦点是
1的右焦点是 ,右顶点是
,右顶点是 ,虚轴的上端点是
,虚轴的上端点是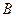 ,
, ,
, .
. 是双曲线上的一点,且过点
是双曲线上的一点,且过点 与
与 轴交于点
轴交于点 ,若
,若 求直线
求直线 的公差是
的公差是 ,
, 是该数列的前
是该数列的前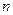 项和.
项和.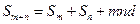 ;
;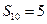 、
、 ,求
,求 ”;
”; 的公比为
的公比为 ,前
,前 ,其中
,其中 的前
的前 项和
项和 .”
.” 粤公网安备 44130202000953号
粤公网安备 44130202000953号