经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: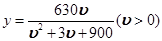 .问:在该时段内,当汽车的平均速度
.问:在该时段内,当汽车的平均速度 等于 时,车流量最大?
等于 时,车流量最大?
某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
t |
70 |
根据上表求出y关于x的线性回归方程为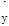 =6.5x+17.5,则表中t的值为_ .
=6.5x+17.5,则表中t的值为_ .
观察分析下表中的数据:
| 多面体 |
面数(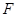 ) ) |
顶点数(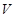 ) ) |
棱数(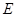 ) ) |
| 三棱锥 |
5 |
6 |
9 |
| 五棱锥 |
6 |
6 |
10 |
| 立方体] |
6 |
8 |
12 |
猜想一般凸多面体中,面数、顶点数、棱数: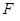 、
、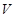 、
、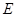 所满足的等式是 .
所满足的等式是 .
某单位为了了解用电量 度与气温
度与气温
 之间的关系,随机统计了某
之间的关系,随机统计了某 天的用电量与当天气温,并制作了对照表
天的用电量与当天气温,并制作了对照表

由表中数据得回归直线方程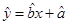 中
中 ,预测当气温为
,预测当气温为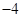
 时,用电量的度数是 .
时,用电量的度数是 .
2015年,各大品牌汽车继续在中国的汽车市场上相互博弈,汽车的配置与销售价格以及维修费用等成为人们购买汽车时需要考虑的因素,某汽车制造商为了进一步拓宽市场,统计了某种品牌的汽车的使用年限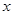 和所支出的维修费用
和所支出的维修费用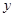 (万元),得到的统计资料:
(万元),得到的统计资料:
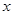 |
2 |
3 |
4 |
5 |
6 |
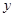 |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料可知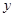 对
对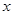 呈线性相关关系,且线性回归方程为
呈线性相关关系,且线性回归方程为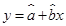 ,其中已知
,其中已知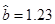 ,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
,根据国家政策规定,轿车取消报废年限,若该品牌汽车在使用10年时报废,则这10年的维修总费用约为_________.
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题某汽车销售公司作了一次抽样调查,并统计得出某款车的使用年限x与所支出的总费用y(万元)有如下的数据资料:
| 使用年限 |
x |
2 |
3 |
4 |
5 |
6 |
| 总费用 |
y |
2.3 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料,知y对x呈线性相关关系.试求:线性回归方程 =
=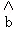 x+
x+ 的回归直线.
的回归直线. =
=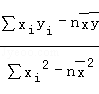 ,
, =
=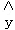 ﹣
﹣
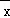 .
.
欲知作者的性别是否与读者的性别有关,某出版公司派人员到各书店随机调查了500位买书的顾客,结果如下:
| 作家 读者 |
男作家 |
女作家 |
合计 |
| 男读者 |
142 |
122 |
264 |
| 女读者 |
103 |
133 |
236 |
| 合计 |
245 |
255 |
500 |
则作者的性别与读者的性别 (填“有关”或“无关”)。
在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘得到如下信息:
| 时间 |
油耗(升/100公里) |
可继续行驶距离(公里) |
| 10:00 |
9.5 |
300 |
| 11:00 |
9.6 |
220 |
注: ,
,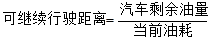 ,
,
 .
.
从以上信息可以推断在10:00—11:00这一小时内 (填上所有正确判断的序号).
行驶了80公里;
行驶不足80公里;
平均油耗超过9.6升/100公里;
平均油耗恰为9.6升/100公里;
平均车速超过80公里/小时.
下表是某厂1~4月份用水量(单位:百吨)的一组数据:
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
由其散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是
 =-0.7x+
=-0.7x+ ,则
,则 = .
= .
某次测量发现一组数据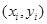 具有较强的相关性,并计算得
具有较强的相关性,并计算得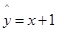 ,其中数据
,其中数据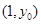 ,Y)因书写不清,只记得
,Y)因书写不清,只记得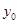 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
某池塘中野生水葫芦的面积与时间的函数关系的图象,如图所示.假设其关系为指数函数,并给出下列说法:

①此指数函数的底数为 ;
;
②在第 个月时,野生水葫芦的面积就会超过
个月时,野生水葫芦的面积就会超过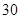
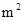 ;
;
③野生水葫芦从
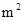 蔓延到
蔓延到
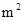 只需
只需 个月;
个月;
④设野生水葫芦蔓延到
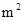 ,
,
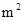 ,
,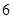
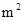 所需的时间分别为
所需的时间分别为 ,
, ,
,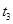 ,则有
,则有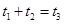 ;
;
⑤野生水葫芦在第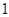 到第
到第 个月之间蔓延的平均速度等于在第
个月之间蔓延的平均速度等于在第 到第
到第 个月之间蔓延的平均速度.
个月之间蔓延的平均速度.
其中正确的说法有 .(请把正确说法的序号都填在横线上)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.根据收集到的数据(如下表),由最小二乘法示得回归直线方程为 。
。
零件数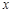 (个) (个) |
10 |
20 |
30 |
40 |
50 |
加工时间 |
62 |
|
75 |
81 |
89 |
表中有一个数据模糊不清,经推断,该数据的值为 .
某次测量发现一组数据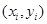 具有较强的相关性,并计算得
具有较强的相关性,并计算得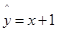 ,其中数据
,其中数据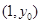 ,Y)因书写不清,只记得
,Y)因书写不清,只记得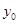 是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)
是[0,3]内的任意一个值,则该数据对应的残差的绝对值不大于l的概率为__________.(残差=真实值一预测值)