根据如下样本数据得到的回归方程为 ,则
,则
 |
3 |
4 |
5 |
6 |
7 |
8 |
 |
 |
 |
 |
 |
 |
 |
A. ,
, B.
B. ,
, C.
C. ,
, D.
D. ,
,
如果散点图中所有的样本点均在同一条直线上,那么残差平方和与相关系数分别为 ( )
| A.1,0 | B.0,1 | C.0.5,0.5 | D.0.43,0.57 |
在一组样本数据 的散点图中,若所有样本点 都在直线 上,则这组样本数据的样本相关系数为()
| A. | -1 | B. | 0 | C. | D. | 1 |
下面是一个2×2列联表: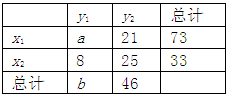
则表中a、b处的值分别为 ( )
| A.94、96 | B.52、50 | C.52、60 | D.54、52 |
已知x、y之间的一组数据如下:
| x |
0 |
1 |
2 |
3 |
| y |
8 |
2 |
6 |
4 |
则线性回归方程 所表示的直线必经过点( )
所表示的直线必经过点( )
A.(0,0) B.(1.5,5) C.(4,1.5) D.(2,2)
如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图,现已知年龄 在[30,35),[35,40),[40,45]的上网人数呈现递减的等差数列,则年龄在[35,40)的频率( )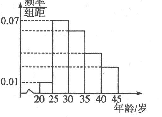
| A.0.04 |
| B.0.06 |
| C.0.2 |
| D.0.3 |
已知x,y取值如表:
| x |
0 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.0 |
9.3 |
9.1 |
从所得的散点图分析可知,y与x线性相关,且y=0.95x+a,则a=( )
A.1.30 B.1.45 C.1.65 D.1.80
已知y与x线性相关,其回归直线的斜率的估计值为1.23,样本的中心点为(4,5),则其回归直线方程为( )
A. |
B. |
C. |
D. |
已知 与
与 之间的几组数据如下表:
之间的几组数据如下表:
 |
1 |
2 |
3 |
4 |
5 |
6 |
 |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程为 .若某同学根据上表中前两组数据
.若某同学根据上表中前两组数据 和
和 求得的直线方程为
求得的直线方程为 ,则以下结论正确的是( )。
,则以下结论正确的是( )。
A. B.
B. C.
C. D.
D.
为研究变量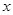 和
和 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程 和
和 ,两人计算知
,两人计算知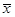 相同,
相同,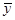 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 与 与 重合 重合 |
B. 与 与 一定平行 一定平行 |
C. 与 与 相交于点 相交于点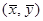 |
D.无法判断 和 和 是否相交 是否相交 |
将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场作的9个分数的茎叶图,后来有1个数据模糊,无法辨认,在图中以x表示,则7个剩余分数的方差为( )
A. |
B. |
C.36 | D.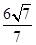 |
下列两个变量之间是相关关系的是( )
| A.圆的面积与半径 | B.球的体积与半径 |
| C.角度与它的正弦值 | D.一个考生的数学成绩与物理成绩 |
观察下列关于变量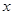 和
和 的三个散点图,它们从左到右的对应关系依次是( )
的三个散点图,它们从左到右的对应关系依次是( )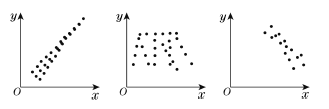
| A.正相关、负相关、不相关 | B.负相关、不相关、正相关 |
| C.负相关、正相关、不相关 | D.正相关、不相关、负相关 |
对于两个变量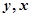 进行回归分析时,分别选择了4个模型,它们的相关指数
进行回归分析时,分别选择了4个模型,它们的相关指数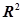 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A.模型1,相关指数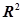 为0.89 为0.89 |
B.模型2,相关指数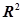 为0.98 为0.98 |
C.模型3,相关指数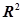 为0.09 为0.09 |
D.模型4,相关指数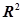 为0.50 为0.50 |