有关线性回归的说法,不正确的是( )
| A.相关关系的两个变量不是因果关系 |
| B.散点图能直观地反映数据的相关程度 |
| C.回归直线最能代表线性相关的两个变量之间的关系 |
| D.任一组数据都有回归方程 |
某班主任对全班50名学生进行了作业量多少的调查,数据如下表:
| |
认为作业多 |
认为作业不多 |
总数 |
| 喜欢玩电脑游戏 |
18 |
9 |
27 |
| 不喜欢玩电脑游戏 |
8 |
15 |
23 |
| 总数 |
26 |
24 |
50 |
算得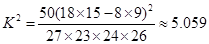 .
.
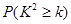 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
3.841 |
5.024 |
6.635 |
10.828 |
附表:
参照附表,得到的正确结论是
A.有 的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;
B.有 的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
C.在犯错误的概率不超过 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少无关系”;
D.在犯错误的概率不超过 的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
的前提下,认为“喜欢玩电脑游戏与认为作业量的多少有关系”.
为了评价某个电视栏目的改革效果,在改革前后分别从居民点抽取了100位居民进行调查,经过计算K2≈0.99,根据这一数据分析,下列说法正确的是
| A.有99%的人认为该栏目优秀 |
| B.有99%的人认为该栏目是否优秀与改革有关系 |
| C.有99%的把握认为电视栏目是否优秀与改革有关系 |
| D.没有理由认为电视栏目是否优秀与改革有关系 |
一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93,用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A.身高一定是145.83cm | B.身高在145.83cm以上 |
| C.身高在145.83cm以下 | D.身高在145.83cm左右 |
设(x1,y1),(x2,y2),…,(xn,yn),是变量x:和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是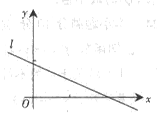
| A. x;和y正相关 |
| B. x和y的相关系数为直线l的斜率 |
| C. x和y的相关系数在-1到0之间 |
| D.当n为偶数时,分布在l两侧的样本点的个数一定相同 |
有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;
③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积;
⑤汽车的重量和百公里耗油量.
其中两个变量成正相关的是( )
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
在下列各图中,每个图的两个变量具有线性相关关系的图是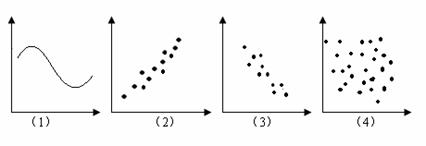
| A.(1)(2) |
| B.(1)(3) |
| C.(2)(4) |
| D.(2)(3) |
有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计得到了一个热饮杯数与当天气温之间的线性关系,其回归方程为 .如果某天气温为-2
.如果某天气温为-2 时,则该小卖部大约能卖出热饮的杯数是
时,则该小卖部大约能卖出热饮的杯数是
| A.140 |
| B.143 |
| C.152 |
| D.156 |
在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( )
| A.总偏差平方和 | B.残差平方和 | C.回归平方和 | D.相关指数R2 |
某车间加工零件的数量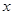 与加工时间
与加工时间 的统计数据如下表:
的统计数据如下表:
零件数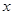 (个) (个) |
10 |
20 |
30 |
加工时间 (分钟) (分钟) |
21 |
30 |
39 |
现已求得上表数据的回归方程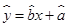 中的
中的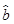 值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
值为0.9,则据此回归模型可以预测,加工100个零件所需要的加工时间约为( )
A.84分钟 B.94分钟 C.102分钟 D.112分钟
已知回归直线的斜率的估计值为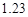 ,样本点的中心为
,样本点的中心为 ,则回归直线方程为
,则回归直线方程为
A.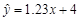 |
B.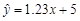 |
C.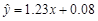 |
D. |
通过随机询问110名性别不同的人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由K2= ,得K2=
,得K2=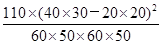 ≈7.8.
≈7.8.
附表:
| P(K2≥k0) |
0.050 |
0.010 |
0.001 |
| k0 |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论 ( ).
A.有99%以上的把握认为“选择过马路的方式与性别有关”
B.有99%以上的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A.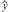 =-10x+200 =-10x+200 |
B.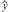 =10x+200 =10x+200 |
C.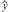 =-10x-200 =-10x-200 |
D. =10x-200 =10x-200 |