2014年高考数学(理)二轮专题复习知能提升演练1-7-3练习卷
某工厂甲、乙、丙三个车间生产了同一种产品,数量分别为120件,80件,60件.为了解它们的产品质量是否存在显著差异,用分层抽样方法抽取了一个容量为n的样本进行调查,其中从丙车间的产品中抽取了3件,则n等( ).
| A.9 | B.10 | C.12 | D.13 |
以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分)
已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( ).
| A.2,5 | B.5,5 | C.5,8 | D.8,8 |
对一批产品的长度(单位:mm)进行抽样检测,下图为检测结果的频率分布直方图.根据标准,产品长度在区间[20,25)上的为一等品,在区间[15,20)和区间[25,30)上的为二等品,在区间[10,15)和[30,35)上的为三等品.用频率估计概率,现从该批产品中随机抽取一件,则其为二等品的概率为 ( ).
| A.0.09 | B.0.20 | C.0.25 | D.0.45 |
通过随机询问110名性别不同的人,对过马路是愿意走斑马线还是愿意走人行天桥进行抽样调查,得到如下的列联表:
| |
男 |
女 |
总计 |
| 走天桥 |
40 |
20 |
60 |
| 走斑马线 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
由K2= ,得K2=
,得K2=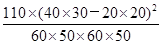 ≈7.8.
≈7.8.
附表:
| P(K2≥k0) |
0.050 |
0.010 |
0.001 |
| k0 |
3.841 |
6.635 |
10.828 |
参照附表,得到的正确结论 ( ).
A.有99%以上的把握认为“选择过马路的方式与性别有关”
B.有99%以上的把握认为“选择过马路的方式与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“选择过马路的方式与性别无关”
已知x与y之间的几组数据如下表:
| x |
1 |
2 |
3 |
4 |
5 |
6 |
| y |
0 |
2 |
1 |
3 |
3 |
4 |
假设根据上表数据所得线性回归直线方程 =
= x+
x+ ,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
,若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( ).
A. >b′,
>b′, >a′ B.
>a′ B. >b′,
>b′, <a′
<a′
C. <b′,
<b′, >a′ D.
>a′ D. <b′,
<b′, <a′
<a′
某学员在一次射击测试中射靶10次,命中环数如下:
7,8,7,9,5,4,9,10,7,4
则(1)平均命中环数为________;(2)命中环数的标准差为________.
如图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为[20.5,21.5),[21.5,22.5),[22.5,23.5),[23.5,24.5),[24.5,25.5),[25.5,26.5].已知样本中平均气温低于22.5 ℃的城市个数为11,则样本中平均气温不低于25.5 ℃的城市个数为________.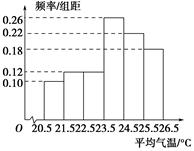
某种产品的广告费支出x与销售额y之间有如下对应数据(单位:百万元).
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
t |
70 |
根据上表提供的数据,求出y关于x的线性回归方程为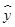 =6.5x+17.5,则表中t的值为________.
=6.5x+17.5,则表中t的值为________.
为了比较两种治疗失眠症的药(分别称为A药,B药)的疗效,随机地选取20位患者服用A药,20位患者服用B药,这40位患者在服用一段时间后,记录他们日平均增加的睡眠时间(单位:h),试验的观测结果如下:
服用A药的20位患者日平均增加的睡眠时间:
0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5
2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4
服用B药的20位患者日平均增加的睡眠时间:
3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4
1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5
(1)分别计算两组数据的平均数,从计算结果看,哪种药的疗效更好?
(2)根据两组数据完成下面茎叶图,从茎叶图看,哪种药的疗效更好?
某工科院校对A,B两个专业的男女生人数进行调查,得到如下的列联表:
| |
专业A |
专业B |
总计 |
| 女生 |
12 |
4 |
16 |
| 男生 |
38 |
46 |
84 |
| 总计 |
50 |
50 |
100 |
(1)从B专业的女生中随机抽取2名女生参加某项活动,其中女生甲被选到的概率是多少?
(2)能否在犯错误的概率不超过0.05的前提下,认为工科院校中“性别”与“专业”有关系呢?
注:K2=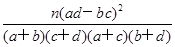
| P(K2≥k0) |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
| k0 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
经销商经销某种农产品,在一个销售季度内,每售出1 t该产品获利润500元,未售出的产品,每1 t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了130 t该农产品.以X(单位: t,100≤X≤150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内经销该农产品的利润.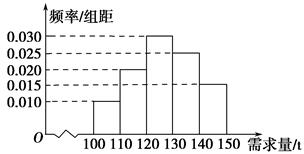
(1)将T表示为X的函数;
(2)根据直方图估计利润T不少于57 000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x∈[100,110),则取X=105,且X=105的概率等于需求量落入[100,110)的频率,求T的数学期望.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号