已知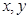 之间的一组数据如下表:
之间的一组数据如下表:
| x |
2 |
3 |
4 |
5 |
6 |
| y |
3 |
4 |
6 |
8 |
9 |
若若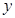 对
对 呈线性相关关系,则回归直线方程为( )
呈线性相关关系,则回归直线方程为( )
A. B.
B. 
C. 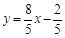 D.
D. 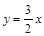
.有下列数据下列四个函数中,模拟效果最好的为( )
| x |
1 |
2 |
3 |
| y |
3 |
5.99 |
12.01 |
A.y=3×2x-1 B.y=log2x
C.y=3x D.y=x2
右表提供了某厂生产某种产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.根据右表提供的数据,求出y关于x的线性回归方程为 =0.7x+0.35,那么表中t的值为( )
=0.7x+0.35,那么表中t的值为( )
| A.3 | B.3.15 | C.3.5 | D.4.5 |
某食品的保鲜时间
(单位:小时)与储藏温度
(单位:
)满足函数关系
(
为自然对数的底数,
为常数).若该食品在
的保鲜时间是
小时,在
的保鲜时间是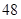 小时,则该食品在
的保鲜时间是()
小时,则该食品在
的保鲜时间是()
| A. | 16小时 | B. | 20小时 | C. | 24小时 | D. | 21小时 |
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 | B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 | D.变量x 与y 负相关,u 与v 负相关 |
设有一个直线回归方程为 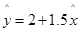 ,则变量x 增加一个单位时( )
,则变量x 增加一个单位时( )
| A.y 平均增加 1.5 个单位 | B.y 平均增加 2 个单位 |
| C.y 平均减少 1.5 个单位 | D.y 平均减少 2 个单位 |
关于相关系数r,下列说法中正确的有:
①若 ,则
,则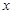 增大时,
增大时, 也相应增大;
也相应增大;
②若 ,则
,则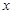 增大时,
增大时, 也相应增大;
也相应增大;
③若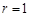 ,或
,或 ,则
,则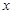 与
与 的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.( )
的关系完全对应(有函数关系),在散点图上各个散点均在一条直线上.( )
| A.①② | B.②③ | C.①③ | D.①②③ |
某商品销售量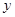 (件)与销售价格
(件)与销售价格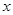 (元/件)负相关,则其回归方程可能是( )
(元/件)负相关,则其回归方程可能是( )
A. =-10x+200 =-10x+200 |
B. =10x+200 =10x+200 |
C. =-10x-200 =-10x-200 |
D. =10x-200 =10x-200 |
工人月工资(元)依劳动产值(千元)变化的回归直线方程为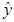 =60+90x,下列判断正确的是( )
=60+90x,下列判断正确的是( )
| A.劳动产值为1 000元时,工资为50元 |
| B.劳动产值提高1 000元时,工资提高150元 |
| C.劳动产值提高1 000元时,工资提高90元 |
| D.劳动产值为1 000元时,工资为90元 |
废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+3x,表明( )
| A.废品率每增加1%,生铁成本增加259元. | B.废品率每增加1%,生铁成本增加3元. |
| C.废品率每增加1%,生铁成本每吨增加3元. | D.废品率不变,生铁成本为256元. |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%,生铁成本平均每吨增加2元 |
已知x,y取值如下表:
| x |
0 |
1 |
4 |
5 |
6 |
8 |
| y |
1.3 |
1.8 |
5.6 |
6.1 |
7.4 |
9.3 |
从所得的散点图分析可知:y与x线性相关,且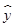 =0.95x+a,则a=( ).
=0.95x+a,则a=( ).
A.1.30 B.1.45 C.1.65 D.1.80
某商品销售量y(件)与销售价格x(元/件)负相关,则其回归方程可能是( )
A.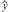 =-10x+200 =-10x+200 |
B.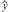 =10x+200 =10x+200 |
C.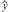 =-10x-200 =-10x-200 |
D.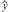 =10x-200 =10x-200 |
已知回归直线的斜率的估计值是 ,样本点的中心为
,样本点的中心为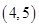 ,则回归直线方程是( )
,则回归直线方程是( )
A. |
B.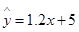 |
C. |
D. |