下表是某厂1到4月份用水量情况(单位:百吨)的一组数据
| 月份x |
1 |
2 |
3 |
4 |
| 用水量y |
4.5 |
4 |
3 |
2.5 |
用水量y与月份x之间具有线性相关关系,其线性回归方程为 ,则a的值为( )
,则a的值为( )
| A.5.25 | B. |
C.2.5 | D.3.5 |
已知x与y之间的一组数据
| x |
0 |
1 |
2 |
3 |
| y |
1 |
3 |
5 |
7 |
(1)画出散点图
(2)若 x与y线性相关,写出线性回归方程必定经过的点
x与y线性相关,写出线性回归方程必定经过的点
(3)若x与y线性相关求出线性回归方程,
(4)说出2个刻画回归效果的手段,假设R =0.74
=0.74 说明什么问题。
说明什么问题。
参考公式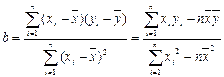
设有一个回归直线方程 ,则变量x增加1个单位时
,则变量x增加1个单位时
| A.y平均增加1.5个单位 | B.y平均增加2个单位 |
| C.y平均减少1.5个单位 | D.y平均减少2个单位 |
.已知 关于
关于 的回归方程为
的回归方程为 ,则变量
,则变量 减少一个单位时( )
减少一个单位时( )
A. 平均增加1.5个单位 平均增加1.5个单位 |
B. 平均增加2个单位 平均增加2个单位 |
C. 平均减少1.5个单位 平均减少1.5个单位 |
D. 平均减少2个单位 平均减少2个单位 |
一位母亲记录了儿子3~9岁 的身高,由此建立的身高与年龄的回归模型为
的身高,由此建立的身高与年龄的回归模型为 =" 7.19" x +73.93. 用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
=" 7.19" x +73.93. 用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
| A.身高一定是145.83 cm; | B.身高在145.83 cm以上; |
| C.身高在145.83 cm以下; | D.身高在145.83 cm左右. |
下列命题中叙述错误的是( )
A. , , |
|
| B.回归分析中,残差平方和越小的模型拟合效果越好 | |
C.r越大, 也越大 也越大 |
D.预报变量与解释变量和随机误差的总效应有关 |
.已知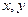 的取值如下表所示:
的取值如下表所示:
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析, 与
与 线性相关,且
线性相关,且 ,由此预测当
,由此预测当
 时,
时, .
.
.已知甲、乙、丙三种食物的维生素A、B含量及成本如下表,若用甲、乙、丙三种食物各x千克,y千克,z千克配成100千克混合食物,并使混合食物内至少含有56000单位维生素A和63000单位维生素B.
| |
甲 |
乙 |
丙 |
| 维生素A(单位/千克) |
600 |
700 |
400 |
| 维生素B(单位/千克) |
800 |
400 |
500 |
| 成本(元/千克) |
11 |
9 |
4 |
(Ⅰ)用x,y表示混合食物成本c元;
(Ⅱ)确定x,y,z的值,使成本最低.
、已知 的取值如下表所示:
的取值如下表所示:
| x |
0 |
1 |
3 |
4 |
| y |
2.2 |
4.3 |
4.8 |
6.7 |
从散点图分析, 与
与 线性相关,且
线性相关,且 ,以此预测当
,以此预测当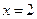 时,
时, .
.
下列说法错误的是( )
| A.自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系叫做相关关系; |
| B.线性回归方程对应的直线=x+至少经过点其样本数据(x1,y1),(x2,y2),…,(xn,yn)中的一个点; |
| C.在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高; |
D.在回归分析中, 为0.98的模型比 为0.98的模型比 为0.80的模型拟合的效果好. 为0.80的模型拟合的效果好. |