已知二次函数 的x与y的部分对应值如下表:
的x与y的部分对应值如下表:
| x |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
| y |
11 |
|
1 |
-1 |
-1 |
1 |
5 |
且方程 的两根分别为
的两根分别为 、
、 ,下面说法错误的是( ) .
,下面说法错误的是( ) .
A. B.
B.
C.当 时,
时, D.当
D.当 时,
时, 有最小值
有最小值
有五组变量:①汽车的重量和汽车每消耗1升汽油所行驶的平均路程;
②平均日学习时间和平均学习成绩;③某人每日吸烟量和其身体健康情况;
④正方形的边长和面积; ⑤汽车的重量和百公里耗油量;
其中两个变量成正相关的是( )
| A.①③ | B.②④ | C.②⑤ | D.④⑤ |
已知回归直线的斜率的估计值为1.23,样本点的中心为(4,5),则回归直线方程为
A.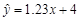 |
B.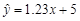 |
C. |
D. |
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验.
根据收集到的数据(如下表),由最小二乘法求得回归方程 .
.
现发现表中有一个数据模糊看不清,请你推断出该数据的值为 .
下表提供了某厂节能降耗技术发行后,生产甲产品过程中记录的产量 (吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
(吨)与相应的生产能耗y(吨标准煤)的几组对应数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)求线性回归方程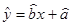 所表示的直线必经过的点;
所表示的直线必经过的点;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程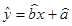 ;
;
并预测生产1000吨甲产品的生产能耗多少吨标准煤?
(参考: )
)
为了考察两个变量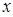 和
和 之间的线性相关性,甲、乙两位同学各自独立地做10次和15
之间的线性相关性,甲、乙两位同学各自独立地做10次和15
次试验,并且利用线性回归方法,求得回归直线分别为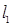 和
和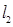 ,已知两个人在试验中发现对
,已知两个人在试验中发现对
变量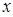 的观测数据的平均值都是
的观测数据的平均值都是 ,对变量
,对变量 的观测数据的平均值都是
的观测数据的平均值都是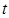 ,那么下列说法正
,那么下列说法正
确的是( )
A.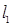 和 和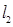 有交点( 有交点( , ,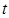 ) ) |
B.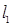 与 与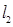 相交,但交点不一定是( 相交,但交点不一定是( , ,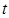 ) ) |
C.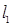 与 与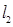 必定平行 必定平行 |
D.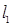 与 与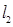 必定重合 必定重合 |
某食品的保鲜时间
(单位:小时)与储藏温度
(单位:
)满足函数关系
(
为自然对数的底数,
为常数).若该食品在
的保鲜时间是
小时,在
的保鲜时间是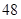 小时,则该食品在
的保鲜时间是()
小时,则该食品在
的保鲜时间是()
| A. | 16小时 | B. | 20小时 | C. | 24小时 | D. | 21小时 |
下列判断中不正确的是( )
A. 为变量间的相关系数, 为变量间的相关系数, 值越大,线性相关程度越高 值越大,线性相关程度越高 |
| B.在平面直角坐标系中,可以用散点图发现变量之间的变化规律 |
C.线性回归方程代表了观测值 、 、 之间的关系 之间的关系 |
| D.任何一组观测值都能得到具有代表意义的回归直线方程 |
下列函数中,随x(x>0)的增大,增长速度最快的是( )
| A.y =1,x∈Z | B.y=x | C.y=  |
D.y=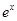 |
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为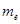 ,众数为
,众数为 ,平均值为
,平均值为 ,则( )
,则( )
A. 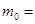  |
B. 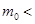  |
C. 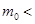  |
D.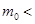   |
废品率 和每吨生铁成本
和每吨生铁成本 (元)之间的回归直线方程为
(元)之间的回归直线方程为 ,这表明 ( )
,这表明 ( )
A. 与 与 的相关系数为2 的相关系数为2 |
B. 与 与 的关系是函数关系的充要条件是相关系数为1 的关系是函数关系的充要条件是相关系数为1 |
| C.废品率每增加1%,生铁成本增加258元 |
| D.废品率每增加1%,生铁成本平均每吨增加2元 |
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
附:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
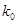 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |