已知函数f(x)是定义在R上不恒为零的函数,且对于任意实数a,b∈R,满足:  (ab)= a
(ab)= a (b)+b
(b)+b (a),
(a),  (2)="2," an=
(2)="2," an= (n∈N*), bn=
(n∈N*), bn= (n∈N*).
(n∈N*).
考察下列结论: ① (0)=
(0)=  (1);②
(1);② (x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
(x)为偶函数; ③数列{an}为等比数列; ④数列{bn}为等差数列.其中正确的结论共有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
数列 满足
满足 并且
并且 ,则数列
,则数列 的第100项为()
的第100项为()
A. |
B. |
C. |
D. |
等比数列{an}各项均为正数,且a1, a3,a2成等差数列,则
a3,a2成等差数列,则 =( ).
=( ).
A. |
B. |
C. |
D. |
数列{an}满足an+1+(﹣1)nan=2n﹣1,则{an}的前60项和为( )
| A.3690 | B.3660 | C.1845 | D.1830 |
已知等差数列 的首项为
的首项为 ,公差为
,公差为 ,且方程
,且方程 的解为
的解为 ,则数列{
,则数列{ }的前n项和
}的前n项和 为( )
为( )
A. |
B. |
C. |
D. |
已知等差数列 的首项为
的首项为 ,公差为
,公差为 ,其前n项和为
,其前n项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则数列
对称,则数列 的前10项和=()
的前10项和=()
A. |
B. |
C. |
D.2 |
已知数列 是正项等差数列,若
是正项等差数列,若 ,则数列
,则数列 也为等差数列.已知数列
也为等差数列.已知数列 是正项等比数列,类比上述结论可得
是正项等比数列,类比上述结论可得
A.若 满足 满足 ,则 ,则 也是等比数列 也是等比数列 |
B.若 满足 满足 ,则 ,则 也是等比数列 也是等比数列 |
C.若 满足 满足 ,则 ,则 也是等比数列 也是等比数列 |
D.若 满足 满足 ,则 ,则 也是等比数列 也是等比数列 |
设等差数列 满足
满足 ,公差
,公差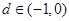 ,当且仅当
,当且仅当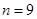 时,数列
时,数列 的前
的前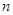 项和
项和 取得最大值,求该数列首项
取得最大值,求该数列首项 的取值范围()
的取值范围()
A.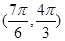 |
B. |
C.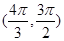 |
D.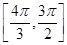 |